题目内容
6.在三棱锥P-ABC中,底面ABC是等腰三角形,∠BAC=120°,BC=2$\sqrt{3}$,PA⊥平面ABC,若三棱锥P-ABC的外接球的表面积为24π,则该三棱锥的体积为$\frac{2\sqrt{6}}{3}$.分析 作出草图,根据底面△ABC与截面圆的关系计算截面半径,根据球的面积计算球的半径,利用勾股定理计算球心到截面的距离,得出棱锥P-ABC的高.
解答 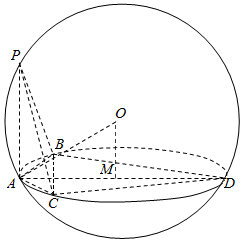 解过A作平面ABC所在球截面的直径AD,连结BD,CD,
解过A作平面ABC所在球截面的直径AD,连结BD,CD,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=∠ADC=∠ADB=30°.
∴∠BCD=∠CBD=∠BDC=60°.即△BCD是等边三角形.
∵BC=2$\sqrt{3}$,∴AD=1+3=4.
过球心O作OM⊥平面ABC,则M为AD的中点,
∴AM=2.
设外接球半径为r,则4πr2=24π,∴r=$\sqrt{6}$.即OA=$\sqrt{6}$.
∴OM=$\sqrt{2}$.
∵PA⊥平面ABC,
∴PA=2OM=2$\sqrt{2}$.
∴VP-ABC=$\frac{1}{3}×\frac{1}{2}×2\sqrt{3}×1×2\sqrt{2}$=$\frac{2\sqrt{6}}{3}$.
故答案为:$\frac{2\sqrt{6}}{3}$.
点评 本题考查棱柱、棱锥、棱台的体积,考查空间想象能力和思维能力,考查计算能力,是中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
14.有一长、宽分别为50m、30m的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出$15\sqrt{2}m$,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3π}{16}$ | D. | $\frac{12+3π}{32}$ |
15.若a=log0.20.3,b=log0.30.2,c=1,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
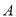 型和20台
型和20台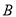 型电脑的利润为4000元,销售20台
型电脑的利润为4000元,销售20台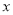 台,这100台电脑的销售总利润为
台,这100台电脑的销售总利润为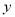 元.
元.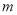 (
(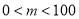 )元,且限定商店最多购进
)元,且限定商店最多购进