题目内容
8.已知集合A={x|x<2},B={x|$\frac{x}{x-1}$<1}R为实数集,则集合A∩(∁RB)=( )| A. | (-∞,2) | B. | (-∞,0] | C. | (1,2) | D. | (-∞,1-$\sqrt{3}$] |
分析 化简集合B,根据补集与交集的定义写出运算结果即可.
解答 解:集合A={x|x<2}=(-∞,2)
由$\frac{x}{x-1}$<1,即$\frac{x}{x-1}$-1<0,即$\frac{1}{x-1}$<0,解得x>1,
B=(1,+∞)
∴∁RB=(-∞,1]
∴A∩(∁RB)=(-∞,2)
故选:A.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
相关题目
3. 执行如图所示的程序框图,输出的a,b的值分别等于( )
执行如图所示的程序框图,输出的a,b的值分别等于( )
 执行如图所示的程序框图,输出的a,b的值分别等于( )
执行如图所示的程序框图,输出的a,b的值分别等于( )| A. | 32,-1 | B. | 32,$\frac{1}{2}$ | C. | 8,1 | D. | 8,-1 |
13.设集合$A=\{\left.x\right|y=\sqrt{2x-{x^2}}\}$,B={y|y=2x,x>0},则A∪B=( )
| A. | (1,2] | B. | [0,+∞) | C. | [0,1)∪(1,2] | D. | [0,2] |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,焦距为2c(c>0),抛物线y2=2cx的准线交双曲线左支于A,B两点,且∠AOB=120°,其中O为原点,则双曲线的离心率为( )
| A. | 2 | B. | $1+\sqrt{2}$ | C. | $1+\sqrt{3}$ | D. | $1+\sqrt{5}$ |
17.已知中心在坐标原点的双曲线的一个焦点与抛物线y=-$\frac{1}{4}$x2的焦点重合,且双曲线的离心率等于$\sqrt{5}$,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{2\sqrt{5}}{5}$x | C. | y=±$\frac{\sqrt{5}}{2}$x | D. | y=±$\frac{1}{2}$x |
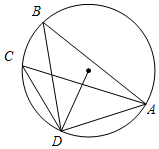 如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.
如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.