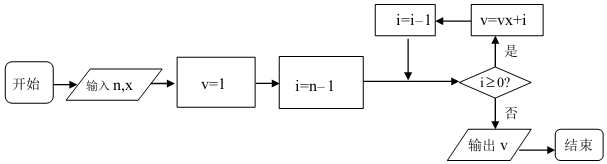
题目内容
7.设函数f(x)=|lgx|,若f(a)=f(b),其中0<a<b,则a+b取值范围是(2,+∞).分析 画出函数f(x)的图象,则数形结合可知0<a<1,b>1,且ab=1,利用基本不等式可求a+b的取值范围.
解答  解:画出y=|lgx|的图象如图:
解:画出y=|lgx|的图象如图:
∵0<a<b,且f(a)=f(b),
∴|lga|=|lgb|且0<a<1,b>1,
∴-lga=lgb,
∴ab=1,
∴a+b≥2$\sqrt{ab}$=2,
∵a≠b,
∴a+b>2,
故答案为:(2,+∞).
点评 本题主要考查了对数函数的图象和性质,利数形结合的思想方法,考查基本不等式的运用,属基础题.

练习册系列答案
相关题目
17.函数f(x)=ln(ex+1)-$\frac{x}{2}$( )
| A. | 是偶函数,但不是奇函数 | B. | 是奇函数,但不是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既不是奇函数,也不是偶函数 |
16.已知定义在R上的函数f(x)=2|x-m|-1(m∈R)为偶函数,记a=f(-2),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
17.已知集合A={x|x≥3或x≤1},B={x|x2-6x+8<0},则(∁RA)∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
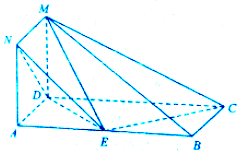 如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.
如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.