题目内容

6．“m=1”是“函数f（x）=log2（1+mx）-log2（1-mx）为奇函数”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

分析 利用函数的奇偶性的判定方法、简易逻辑的判定方法即可得出．

解答 解：函数f（x）=log2（1+mx）-log2（1-mx）为奇函数，则f（-x）+f（x）=log2（1-mx）-log2（1+mx）+log2（1+mx）-log2（1-mx）=0，m，x满足：$\left\{\begin{array}{l}{1+mx＞0}\\{1-mx＞0}\end{array}\right.$．
可得“m=1”是“函数f（x）=log2（1+mx）-log2（1-mx）为奇函数”，反之不成立，例如取m=-1．
因此“m=1”是“函数f（x）=log2（1+mx）-log2（1-mx）为奇函数”的充分不必要条件．
故选：A．

点评 本题考查了简易逻辑的判定方法、函数的奇偶性，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
16．已知定义在R上的函数f（x）=2|x-m|-1（m∈R）为偶函数，记a=f（-2），b=f（log25），c=f（2m），则a，b，c的大小关系为（　　）
A．a＜b＜cB．c＜a＜bC．a＜c＜bD．c＜b＜a
17．已知集合A={x|x≥3或x≤1}，B={x|x2-6x+8＜0}，则（∁RA）∩B=（　　）
A．（1，3）B．（1，4）C．（2，3）D．（2，4）
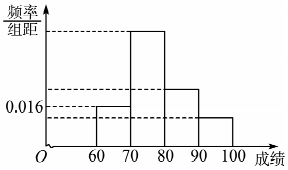14．某班为了提高学生学习英语的兴趣，在班内举行英语写、说、唱综合能力比赛，比赛分为预赛和决赛2个阶段，预赛为笔试，决赛为说英语、唱英语歌曲，将所有参加笔试的同学进行统计，得到频率分布直方图，其中后三个矩形高度之比依次为4：2：1，落在[80，90）的人数为12人．
（Ⅰ）求此班级人数；
（Ⅱ）按规定预赛成绩不低于90分的选手参加决赛，已知甲乙两位选手已经取得决赛资格，参加决赛的选手按抽签方式决定出场顺序．
（i）甲不排在第一位乙不排在最后一位的概率；
（ii）记甲乙二人排在前三位的人数为X，求X的分布列和数学期望．
1．已知$|\overrightarrow a|=1$，$|\overrightarrow a+\overrightarrow b|=\sqrt{7}$，$\overrightarrow a•（\overrightarrow b-\overrightarrow a）=-4$，则$\overrightarrow a$与$\overrightarrow b$夹角是$\frac{5π}{6}$．
11．若$\int_1^e{\frac{2}{x}dx=a}$，则${（{x-\frac{a}{x}}）^6}$展开式中的常数项为-160．
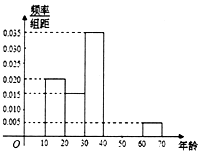18．2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱，某记者调查了部分年龄在[10，70]的观众，得到如下频率分布直方图．若第四、五、六组的人数依次成等差数列，且第六组有4人．
（1）请补充完整频率分布直方图，并估计这组数据的平均数$\overline x$；
（2）现根据观看年龄，从第四组和第六组的所有观众中任意选2人，记他们的年龄分别为x，y，若|x-y|≥10，则称此2人为“最佳诗词搭档”，试求选出的2人为“最佳诗词搭档”的概P；
（3）以此样本的频率当作概率，现随机从这组样本中选出3名观众，求年龄不低于40岁的人数ξ的分布列及期望．
15．在△ABC中，$AB=3，AC=2，\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC}，则\overrightarrow{AD}•\overrightarrow{DB}$的值为（　　）
A．$\frac{5}{2}$B．$-\frac{5}{2}$C．$\frac{5}{4}$D．$-\frac{5}{4}$
16．已知正方体外接球的体积是$\frac{32}{3}π$，那么此正方体的棱长等于$\frac{4\sqrt{3}}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网