题目内容
在△ABC中，点G为△ABC的重心．已知|AB|=2
，且向量
与
的夹角为120°，则
•
的最小值是
（ ）
| 3 |
| GA |
| GB |
| CA |
| CB |
（ ）
| A、-3 | B、6 | C、9 | D、24 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，由
=
+
，
=
+
.
+
=2
.
=2
，可得
•
=8
2+
•
，设GA=m，GB=n．由中线长定理可得：m2+n2=2
2+6．由余弦定理可得：AB2=GA2+GB2-2GA•GBcos120°，即(2
)2=m2+n2-2mn×(-
)，可得mn≤4，即可得出．
| CA |
| CG |
| GA |
| CB |
| CG |
| GB |
| GA |
| GB |
| GD |
| CG |
| GD |
| CA |
| CB |
| GD |
| GA |
| GB |
| GD |
| 3 |
| 1 |
| 2 |
解答：
解：如图所示，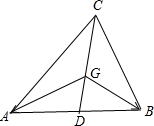
∵
=
+
，
=
+
．
+
=2
．
=2
，
∴
•
=(
+
)•(
+
)
=
2+
(
+
)+
•
=
2+
2+
•
=8
2+
•
，
设GA=m，GB=n．
由中线长定理可得：m2+n2=2
2+6，
∴
•
=4（m2+n2-6）-
mn
≥
mn-24．
由余弦定理可得：AB2=GA2+GB2-2GA•GBcos120°，
∴(2
)2=m2+n2-2mn×(-
)，
化为12=m2+n2+mn≥3mn，当且仅当m=n时取等号．
∴mn≤4，
∴
•
=
×4-24=6，当且仅当m=n=2时取等号．
故选：B．
∵
| CA |
| CG |
| GA |
| CB |
| CG |
| GB |
| GA |
| GB |
| GD |
| CG |
| GD |
∴
| CA |
| CB |
| CG |
| GA |
| CG |
| GB |
=
| CG |
| CG• |
| GA |
| GB |
| GA |
| GB |
=
| CG |
| CG |
| GA |
| GB |
=8
| GD |
| GA |
| GB |
设GA=m，GB=n．
由中线长定理可得：m2+n2=2
| GD |
∴
| CA |
| CB |
| 1 |
| 2 |
≥
| 15 |
| 2 |
由余弦定理可得：AB2=GA2+GB2-2GA•GBcos120°，
∴(2
| 3 |
| 1 |
| 2 |
化为12=m2+n2+mn≥3mn，当且仅当m=n时取等号．
∴mn≤4，
∴
| CA |
| CB |
| 15 |
| 2 |
故选：B．
点评：本题考查了向量的三角形法则、三角形的重心性质、数量积运算性质、余弦定理、中线长定理、基本不等式的性质考查了推理能力与计算能力，属于难题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目