题目内容
19．已知函数$f（x）=-\frac{1}{3}{x^3}+m{x^2}+n（m，n，x∈R）$图象上任意两点A（x1，y1）、B（x2，y2）（x1＞x2），满足$f（{x_1}）-f（{x_2}）＜{x_1}-{x_2}+{x_1}^2-{x_2}^2$，则实数m的取值范围是（ ）| A． | [0，2] | B． | （-∞，0） | C． | （0，2） | D． | [2，+∞] |
分析 由题意得$\frac{1}{3}$x23-mx22+x2+x22＜$\frac{1}{3}$x13-mx12+x1+x12，从而转化为证明g（x）=$\frac{1}{3}$x3-（m-1）x2+x在R上是增函数，求导解出即可．
解答 解：由题意得，
f（x1）=-$\frac{1}{3}$x13+mx12+n，f（x2）=-$\frac{1}{3}$x23+mx22+n，
则（-$\frac{1}{3}$x13+mx12+n）-（-$\frac{1}{3}$x23+mx22+n）＜x1-x2+x12-x22，
则$\frac{1}{3}$x23-mx22+x2+x22＜$\frac{1}{3}$x13-mx12+x1+x12，
即$\frac{1}{3}$x23-（m-1）x22+x2＜$\frac{1}{3}$x13-（m-1）x12+x1，
故g（x）=$\frac{1}{3}$x3-（m-1）x2+x在R上是增函数，
g′（x）=x2-2（m-1）x+1，
故△=4（m-1）2-4×1×1≤0，
解得0≤m≤2．
故选A．
点评 本题考查了函数的单调性的应用及导数的综合应用．
练习册系列答案
阅读快车系列答案
相关题目
7．已知函数f（x）=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$．
（1）若f（x）的定义域为R，求实数a的取值范围；
（2）若f（x）的值域为[0，+∞），求实数a的取值．
（1）若f（x）的定义域为R，求实数a的取值范围；
（2）若f（x）的值域为[0，+∞），求实数a的取值．
4．已知数列{an}满足an+1=an+$\frac{1}{2}$，则数列{an}是（ ）
| A． | 递增数列 | B． | 递减数列 | C． | 摆动数列 | D． | 常数列 |
11．
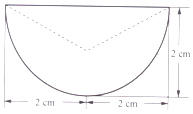某零件的正视图与侧视图均是如图所示的图形（实线组成半径为2cm的半圆，虚线是底边上高为1cm的等腰三角形的两腰），俯视图是一个半径为2cm的圆（包括圆心），则该零件的体积是（ ）
某零件的正视图与侧视图均是如图所示的图形（实线组成半径为2cm的半圆，虚线是底边上高为1cm的等腰三角形的两腰），俯视图是一个半径为2cm的圆（包括圆心），则该零件的体积是（ ）| A． | $\frac{4}{3}πc{m^3}$ | B． | $\frac{8}{3}πc{m^3}$ | C． | 4πcm3 | D． | $\frac{20}{3}πc{m^3}$ |