题目内容
7.已知函数f(x)=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$.(1)若f(x)的定义域为R,求实数a的取值范围;
(2)若f(x)的值域为[0,+∞),求实数a的取值.
分析 (1)根据指数函数以及二次根式的性质求出a的范围即可;
(2)根据函数的值域的范围,得到关于a的方程,求出a的范围即可.
解答 解:(1)若f(x)的定义域为R,
由2x>0,则$\frac{a}{{2}^{x}}$>0,则a>0,
则f(x)=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$≥$\sqrt{2\sqrt{a}-2}$≥0,
解得:a≥1,
故a的范围是[1,+∞);
(2)若f(x)的值域为[0,+∞),
则f(x)=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$≥$\sqrt{2\sqrt{a}-2}$≥0,
由2$\sqrt{a}$-2=0,解得:a=1.
点评 本题考查了函数的定义域、值域问题,考查指数函数的性质以及基本不等式的性质,是一道中档题.

练习册系列答案
相关题目
8.设全集U=R,集合A={x|x>1},集合B={x|x>p},若(∁UA)∩B=∅,则p应该满足的条件是( )
| A. | p>1 | B. | p≥1 | C. | p<1 | D. | p≤1 |
15.若函数f(x)=(a-1)x3+ax2为奇函数,则f(1)=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 0 |
12.已知ω>0,函数$f(x)=sin({ωx-\frac{π}{3}})$在$({\frac{π}{3},\frac{π}{2}})$上单调递减,则ω的取值范围是( )
| A. | $[{\frac{5}{2},\frac{11}{3}}]$ | B. | $[{\frac{1}{2},\frac{3}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | $({0,\frac{11}{3}}]$ |
19.已知函数$f(x)=-\frac{1}{3}{x^3}+m{x^2}+n(m,n,x∈R)$图象上任意两点A(x1,y1)、B(x2,y2)(x1>x2),满足$f({x_1})-f({x_2})<{x_1}-{x_2}+{x_1}^2-{x_2}^2$,则实数m的取值范围是( )
| A. | [0,2] | B. | (-∞,0) | C. | (0,2) | D. | [2,+∞] |
17.平面α∥平面β,直线a?α,b?β,那么直线a与直线b的位置关系一定是( )
| A. | 平行 | B. | 异面 | C. | 垂直 | D. | 不相交 |
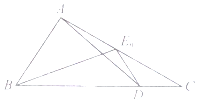 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )