题目内容
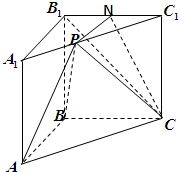 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动(1)试问点P在何处时,AB∥平面PNC,并证明你的结论;
(2)在(1)的条件下,且AA1<AB,直线B1C与平面BCP的成角的正弦值为
| ||
| 10 |
考点:与二面角有关的立体几何综合题,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)点P在A1C1中点位置时,AB∥平面PNC.利用三角形中位线定理和平行公理能推导出AB∥PN,由此能证明AB∥平面PNC.
(2)以B为原点,以BA为x轴,以BC为y轴,以BB1为z轴,建立空间直角坐标系,利用向量法由已知条件能求出AA1的长,由此利用向量法能求出二面角A-BP-C的大小.
(2)以B为原点,以BA为x轴,以BC为y轴,以BB1为z轴,建立空间直角坐标系,利用向量法由已知条件能求出AA1的长,由此利用向量法能求出二面角A-BP-C的大小.
解答:
解:(1)点P在A1C1中点位置时,AB∥平面PNC.
证明如下:
∵在三棱柱ABC-A1B1C1中,点N为B1C1的中点,点P在棱A1C1的运动,
∴点P在A1C1中点位置时,PN是△A1B1C1的中位线,
∴PN∥A1B1,
∵AB∥A1B1,∴AB∥PN,
∵AB不包含于平面PNC,PN?平面PNC,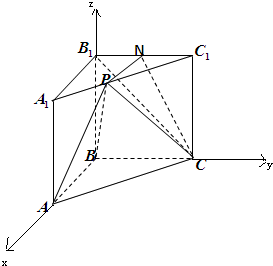
∴AB∥平面PNC.
(2)在三棱柱ABC-A1B1C1中,
∵AA1⊥平面ABC,AB⊥BC,
∴以B为原点,以BA为x轴,以BC为y轴,以BB1为z轴,
建立空间直角坐标系,
∵AB=BC=2,点N为B1C1的中点,点P为A1C1的中点,设AA1=λ,
∴B(0,0,0),A1(2,0,λ),C1(0,2,λ),C(0,2,0),
B1(0,0,λ),A(2,0,0),
∴P(1,1,λ),
=(1,1,λ),
=(0,2,0),
=(0,-2,λ),
=(2,0,0),
设平面BPC的法向量为
=(x,y,z),
则
,∴
=(λ,0,-1),
∵直线B1C与平面BCP的成角的正弦值为
,
∴|cos<
,
>|=|
|=
解得λ=±1或λ=±2,
∵AA1<AB,∴λ=1,
∴AA1=1,平面BPC的法向量
=(1,0,-1),
=(1,1,1).
设平面ABP的法向量
=(x1,y1,z1),
则
,∴
=(0,1,-1),
设二面角A-BP-C的平面角为θ,
则cosθ=-|cos<
,
>|=-|
|=-
,
∴θ=120°.
∴二面角A-BP-C的大小为120°.
证明如下:
∵在三棱柱ABC-A1B1C1中,点N为B1C1的中点,点P在棱A1C1的运动,
∴点P在A1C1中点位置时,PN是△A1B1C1的中位线,
∴PN∥A1B1,
∵AB∥A1B1,∴AB∥PN,
∵AB不包含于平面PNC,PN?平面PNC,

∴AB∥平面PNC.
(2)在三棱柱ABC-A1B1C1中,
∵AA1⊥平面ABC,AB⊥BC,
∴以B为原点,以BA为x轴,以BC为y轴,以BB1为z轴,
建立空间直角坐标系,
∵AB=BC=2,点N为B1C1的中点,点P为A1C1的中点,设AA1=λ,
∴B(0,0,0),A1(2,0,λ),C1(0,2,λ),C(0,2,0),
B1(0,0,λ),A(2,0,0),
∴P(1,1,λ),
| BP |
| BC |
| CB1 |
| BA |
设平面BPC的法向量为
| n |
则
|
| n |
∵直线B1C与平面BCP的成角的正弦值为
| ||
| 10 |
∴|cos<
| n |
| CB1 |
| -λ | ||||
|
| ||
| 10 |
解得λ=±1或λ=±2,
∵AA1<AB,∴λ=1,
∴AA1=1,平面BPC的法向量
| n |
| BP |
设平面ABP的法向量
| n2 |
则
|
| n2 |
设二面角A-BP-C的平面角为θ,
则cosθ=-|cos<
| n1 |
| n2 |
| 0+0+1 | ||||
|
| 1 |
| 2 |
∴θ=120°.
∴二面角A-BP-C的大小为120°.
点评:本题考查直线与平面平行的判断与证明,考查二面角大小的求法,解题时要注意向量法的合理运用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
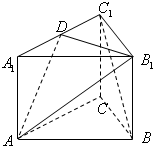 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为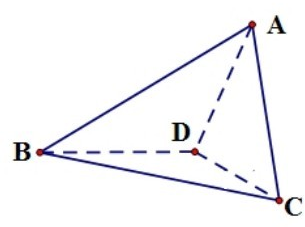 已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.
已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.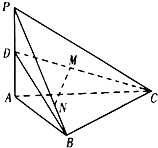 如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2
如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2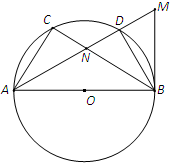 如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.
如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.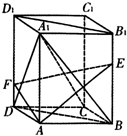 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.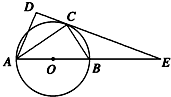 如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.若EB=6,EC=6
如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.若EB=6,EC=6