求函数y=cos2x+sinx,x∈[$\frac{π}{4}.\frac{3π}{4}$]的值域．题目和参考答案——青夏教育精英家教网—

题目内容

15．求函数y=cos2x+sinx；x∈[$\frac{π}{4}，\frac{3π}{4}$]的值域．

分析利用二倍角公式化简得到y关于sinx的二次函数，利用二次函数的性质求出最值．

解答解：y=cos2x+sinx=1-2sin²x+sinx=-2（sinx-$\frac{1}{4}$）²+$\frac{9}{8}$．
∵x∈[$\frac{π}{4}，\frac{3π}{4}$]，∴sinx∈[$\frac{\sqrt{2}}{2}$，1]，
∴当sinx=$\frac{\sqrt{2}}{2}$时，函数y=cos2x+sinx取得最大值$\frac{\sqrt{2}}{2}$，
当sinx=1时，函数y=cos2x+sinx取得最小值0．
∴函数y=cos2x+sinx在[$\frac{π}{4}$，$\frac{3π}{4}$]上的值域为[0，$\frac{\sqrt{2}}{2}$]．

点评本题考查了三角函数的恒等变换，二次函数的性质，属于中档题．

练习册系列答案

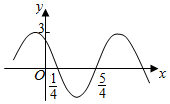
	A．	（kπ-$\frac{5}{4}$，kπ-$\frac{1}{4}$），k∈Z		B．	（2kπ-$\frac{5}{4}$，2kπ-$\frac{1}{4}$），k∈Z
	C．	（2k-$\frac{5}{4}$，2k-$\frac{1}{4}$），k∈Z		D．	（k-$\frac{5}{4}$，k-$\frac{1}{4}$），k∈Z

6．已知a，b，c分别为△ABC三个内角A，B，C的对边，b=acosC+$\frac{\sqrt{3}}{3}$asinC．
（I）求A；
（Ⅱ）若a=2，b+c≥4，求△ABC的面积．

3．（5x-6y）⁵的展开式中二项式系数之和是32．

10．在数列{a_n}中，若a_n+1是a_n和a_n+2的等差中项，数列{a_n}是否是等差数列？说明理由．

3．在区间（0，100）上任取一数x，则lg x＞1的概率是（　　）

10．定义在R上的偶函数f（x）对任意x满足f（x+π）=f（x），且当$x∈[0，\frac{π}{2}]$时，f（x）=sinx，则$f（\frac{5π}{3}）$的值为$\frac{{\sqrt{3}}}{2}$．

7．

如图在正方体ABCD-A₁B₁C₁D₁中，E是棱CC₁的中点．
（Ⅰ）证明：AC₁∥平面BDE；
（Ⅱ）证明：AC₁⊥BD
（Ⅲ）证明：面BDE⊥面ACC₁．

8．已知正三棱柱的底面边长和高都是2，则此三棱柱外接球的表面积为$\frac{28π}{3}$．
′．

试题分类