题目内容
7. 如图在正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
如图在正方体ABCD-A1B1C1D1中,E是棱CC1的中点.(Ⅰ)证明:AC1∥平面BDE;
(Ⅱ)证明:AC1⊥BD
(Ⅲ)证明:面BDE⊥面ACC1.
分析 (I)连接AC交BD于O,连接OE,推导出AC1∥OE,由此能证明AC1∥平面BDE.
(II)推导出AC⊥BD,由此能证明CC1⊥BD.
(Ⅲ)由面ACC1⊥BD,能证明面BDE⊥面ACC1.
解答 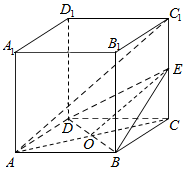 证明:(I)连接AC交BD于O,连接OE
证明:(I)连接AC交BD于O,连接OE
∵ABCD是正方形,∴O为AC的中点,
∵E是棱CC1的中点,∴AC1∥OE,
又∵AC1?平面BDE,OE?平面BDE,
∴AC1∥平面BDE.
(II)∵ABCD是正方形,∴AC⊥BD,
∵CC1⊥平面ABCD,且BD?平面ABCD,
∴CC1⊥BD.
(Ⅲ)由(Ⅱ)得,面ACC1⊥BD,BD?平面BDE,
∴面BDE⊥面ACC1.
点评 本题考查线面平行的证明,考查异面直线垂直的证明,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
15.某辆汽车每次加油都把油箱加满,如表记录了该车相邻两次加油时的情况.
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为8升.
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2015年5月1日 | 12 | 35000 |
| 2015年5月15日 | 48 | 35600 |
在这段时间内,该车每100千米平均耗油量为8升.
 已知正三棱柱ABC-A1B1C1中,D是AB中点,E,F分别为A1D,A1C的中点.
已知正三棱柱ABC-A1B1C1中,D是AB中点,E,F分别为A1D,A1C的中点.