题目内容
已知两圆C1:x2+y2=4,C2:x2+y2-2x-4y+4=0,直线l:x+2y=0,求经过圆C1、C2的交点且和直线l相切的圆的方程.
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:联立方程组求得两个圆的交点,设圆心的坐标为M(a,b),则由MA=MB,还等于M到直线直线l:x+2y=0的距离求得a、b的值,可得圆心和半径MA,从而求得圆的方程.
解答:
解:由
,求得
,或
,
故两个圆的交点为A(0,2)、B(
,
),
设圆心的坐标为M(a,b),则由MA=MB,还等于M到直线直线l:x+2y=0的距离.
可得
=
=
,求得a=
,b=1,故半径MA=
,
故要求的圆的方程为 (x-
)2+(y-1)2=
.
|
|
|
故两个圆的交点为A(0,2)、B(
| 8 |
| 5 |
| 6 |
| 5 |
设圆心的坐标为M(a,b),则由MA=MB,还等于M到直线直线l:x+2y=0的距离.
可得
| a2+(b-2)2 |
(a-
|
| |a+2b| | ||
|
| 1 |
| 2 |
|
故要求的圆的方程为 (x-
| 1 |
| 2 |
| 5 |
| 4 |
点评:本题主要考查求圆的标准方程的方法,直线和圆的位置关系,点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
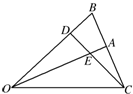 如图所示,已知△AOB中,点C与点B关于点A对称,
如图所示,已知△AOB中,点C与点B关于点A对称,
 已知四棱柱ABCD-A1B1C1D1中所有棱长都为2,底面ABCD为正方形,侧面DD1C1C⊥底面ABCD,∠D1DC=60°
已知四棱柱ABCD-A1B1C1D1中所有棱长都为2,底面ABCD为正方形,侧面DD1C1C⊥底面ABCD,∠D1DC=60° 如图,在△ABC中,∠ABC=90°,AB=
如图,在△ABC中,∠ABC=90°,AB=