题目内容
16.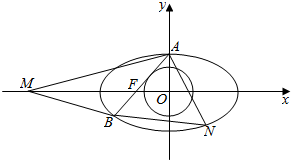 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.(1)求椭圆C1的方程;
(2)设点N为椭圆C1上异于A、B的任意一点,求△ABN面积的最大值;
(3)试探求x轴上是否存在定点M,使得∠AMF=∠BMF,若存在,求点M的坐标,若不存在,则说明理由.
分析 (1)由题意可得A(0,b),F(-c,0),求得直线AB的方程,由直线和圆相切的条件:d=r,以及椭圆的准线方程,解方程可得a,b,进而得到椭圆的方程;
(2)求得A,B的坐标,弦长AB,再设直线y=x+t,代入椭圆方程,由相切的条件判别式为0,可得t,再由平行直线的距离公式可得N到直线的最大距离,即可得到所求面积的最大值;
(3)假设x轴上存在定点M(m,0),使得∠AMF=∠BMF,可得直线AM,BM的斜率互为相反数,运用直线的斜率公式计算即可得到所求点的坐标.
解答 解:(1)由题意可得A(0,b),F(-c,0),
直线AF的方程为cy-bx=bc,
由直线和圆相切的条件可得$\frac{bc}{\sqrt{{b}^{2}+{c}^{2}}}$=$\frac{b}{\sqrt{2}}$,
即有b=c,
又椭圆C1左焦点(-c,0)到左准线x=-$\frac{{a}^{2}}{c}$的距离为1,
可得-c+$\frac{{a}^{2}}{c}$=1,a=$\sqrt{2}$c,
解得a=$\sqrt{2}$,b=c=1,
即有椭圆方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)将直线y=x+1代入椭圆方程,可得B(-$\frac{4}{3}$,-$\frac{1}{3}$),
设与直线y=x+1平行的直线为y=x+t,
当直线y=x+t与椭圆相切时,面积取得最值.
由$\left\{\begin{array}{l}{y=x+t}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$可得3x2+4tx+2t2-2=0,
由△=16t2-12(2t2-2)=0,解得t=±$\sqrt{3}$,
由题意可得直线y=x-$\sqrt{3}$,
即有面积的最大值为$\frac{1}{2}$•|AB|•d=$\frac{1}{2}$•$\frac{4}{3}$$\sqrt{2}$•$\frac{\sqrt{3}+1}{\sqrt{2}}$=$\frac{2}{3}$($\sqrt{3}$+1);
(3)假设x轴上存在定点M(m,0),使得∠AMF=∠BMF,
可得直线AM,BM的斜率互为相反数,
即有$\frac{1-0}{0-m}$=-$\frac{\frac{1}{3}}{\frac{4}{3}+m}$,解方程可得m=-2.
则x轴上存在定点M(-2,0),使得∠AMF=∠BMF.
点评 本题考查椭圆的方程的求法,注意运用直线和圆相切的条件:d=r,考查三角形的面积的最值的求法,注意运用直线和椭圆相切,考查直线的斜率公式的运用,属于中档题.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案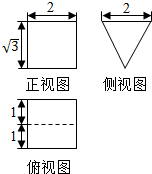
| A. | $12+\sqrt{3}$ | B. | $12+2\sqrt{3}$ | C. | $4+3\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
| A. | 1<x<2 | B. | 1<x<3 | C. | 0<x<3 | D. | 1<x<4 |
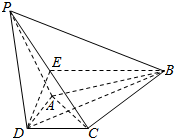 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.