题目内容
13.已知函数f(x)=$\frac{a}{2}$+$\frac{2}{{2}^{x}+1}$是奇函数.(1)求a的值;
(2)判断f(x)的单调性,并用定义加以证明;
(3)求f(x)的值域.
分析 (1)直接根据奇函数的性质f(0)=0,求出a,再进行验证;
(2)先判断函数单调递减,再利用函数单调性的定义用作差比较法证明;
(3)根据指数函数的性质得出函数f(x)的值域.
解答 解:(1)因为f(x)为奇函数,所以f(0)=0,
即$\frac{a}{2}$+$\frac{2}{2}$=0,解得a=-2,
此时,f(x)=$\frac{1-2^x}{1+2^x}$,再验证如下:
f(x)+f(-x)=$\frac{1-2^x}{1+2^x}$+$\frac{1-{2}^{-x}}{1+{2}^{-x}}$=$\frac{1-2^x}{1+2^x}$-$\frac{1-2^x}{1+2^x}$=0,
所以,f(x)为定义域上的奇函数;
(2)因为f(x)=$\frac{2}{2^x+1}$-1,
所以,f(x)为R上的减函数,证明如下:
任取x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=2[$\frac{1}{{2}^{{x}_{1}}}$-$\frac{1}{{2}^{{x}_{2}}}$]=2×$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{{2}^{{x}_{1}+{x}_{2}}}$,
以为,x1<x2,所以f(x1)>f(x2),
因此,f(x)为(-∞,+∞)上的单调递减函数;
(3)因为f(x)=$\frac{2}{2^x+1}$-1,
其中,2x+1∈(1,+∞),所以,$\frac{2}{2^x+1}$∈(0,2),
所以,f(x)∈(-1,1),
因此,f(x)的值域为:(-1,1).
点评 本题主要考查了对数函数的图象与性质的综合应用,涉及函数的奇偶性,单调性,以及函数值域的解法,属于中档题.

练习册系列答案
相关题目
5.下列关系式中表述正确的是( )
| A. | 0∈{(0,0)} | B. | 0∈∅ | C. | 0∈N | D. | {0}∈{x|x2=0} |
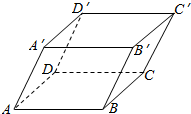 如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量:
如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量: