题目内容
4.设函数$f(x)={log_2}(1+a•{2^x}+{4^x})$,其中a为常数(1)当f(2)=f(1)+2时,求a的值;
(2)当x∈[1,+∞)时,关于x的不等式f(x)≥x-1恒成立,试求a的取值范围;
(3)若a∈R,试求函数y=f(x)的定义域.
分析 (1)直接代入,解方程即可;
(2)不等式可整理为$a≥-{2^x}-\frac{1}{2^x}+\frac{1}{2}$,只需求出右式的最大值即可.利用换元法令t=2x,t∈[2,+∞)
得出$h(t)=-t-\frac{1}{t}+\frac{1}{2}$,根据定义法判断函数的单调性,进而求出函数的最大值;
(3)利用换元法m=2x(m>0)即m2+a•m+1>0,对二次不等式m2+a•m+1>0分类讨论,求出函数的定义域即可.
解答 解:(1).f(2)=f(1)+2⇒log2(1+4a+16)=log2(1+2a+4)+log24⇒log2(17+4a)=log24(5+2a)⇒17+4a=20+8a⇒$a=-\frac{3}{4}$…(3分)
(2)${log_2}(1+a•{2^x}+{4^x})≥x-1={log_2}{2^{x-1}}$1+a•2x+4x≥2x-1⇒$a≥-{2^x}-\frac{1}{2^x}+\frac{1}{2}$
令t=2x∵x∈[1,+∞)∴t∈[2,+∞)
设$h(t)=-t-\frac{1}{t}+\frac{1}{2}$,2≤t1<t2
∴$h({t_1})-h({t_2})=-{t_1}-\frac{1}{t_1}+{t_2}+\frac{1}{t_2}=({t_2}-{t_1})•\frac{{{t_1}{t_2}-1}}{{{t_1}{t_2}}}$
∵(t2-t1)>0,t1t2-1>0,t1t2>0
∴h(t1)>h(t2)
∴h(t)在[2,+∞)上为减函数,
∴t=2时,$y=-t-\frac{1}{t}+\frac{1}{2}$有最大值为-2
∴a≥-2…(8分)
(3)1+a•2x+4x>0⇒
令m=2x(m>0)即m2+a•m+1>0
①当△=a2-4<0⇒-2<a<2m∈R⇒x∈R
②当△=a2-4=0⇒a=2或a=-2
若a=2,(m+1)2>0又m>0⇒x∈R
若a=-2,(m-1)2>0又m≠1⇒x∈{x|x≠0,x∈R}
③当△=a2-4>0⇒a>2或a<-2
设g(m)=m2+a•m+1而g(0)=1>0
若a>2,$-\frac{a}{2}<-1$而m>0⇒x∈R
若a<-2,$-\frac{a}{2}>1$而m>0⇒$0<m<\frac{{-a-\sqrt{{a^2}-4}}}{2}或m>\frac{{-a+\sqrt{{a^2}-4}}}{2}$⇒${2^x}<\frac{{-a-\sqrt{{a^2}-4}}}{2}或{2^x}>\frac{{-a+\sqrt{{a^2}-4}}}{2}$⇒$x<{log_2}\frac{{-a-\sqrt{{a^2}-4}}}{2}或x>{log_2}\frac{{-a+\sqrt{{a^2}-4}}}{2}$
综上:①当a>-2时 f(x)定义域为R
②当a≤-2时f(x)定义域为$(-∞,{log_2}\frac{{-a-\sqrt{{a^2}-4}}}{2})∪({log_2}\frac{{-a+\sqrt{{a^2}-4}}}{2},+∞)$…(14分)
点评 考查了利用换元法和根据函数单调性判断函数的最值,对复合函数,利用对二次不等式的分类讨论求函数的定义域问题.难点是分类讨论.

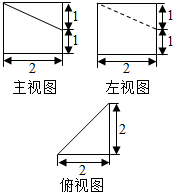
| A. | $\frac{23}{3}$ | B. | 4$\sqrt{2}$+$\sqrt{6}$+6 | C. | 6$\sqrt{2}$+6 | D. | 4$\sqrt{2}$+$\sqrt{6}$+8 |
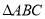 中,
中,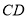 是
是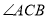 的角平分线,
的角平分线,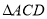 的外接圆交
的外接圆交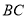 于
于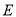 点.
点.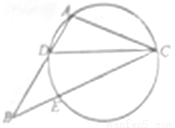
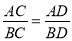 ;
;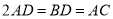 ,求
,求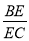 的值.
的值. 已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.
已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.