题目内容
8.不等式|x-3|≥1的解集为(-∞,2]∪[4,+∞).分析 直接去掉绝对值符号,将不等式等价为:x-3≥1或x-3≤-1,解出即可.
解答 解:不等式|x-3|≥1等价为:
x-3≥1或x-3≤-1,
解得,x≥4或x≤2,
即该不等式的解集为:{x|x≥4,或x≤2},
故答案为:(-∞,2]∪[4,+∞).
点评 本题主要考查了绝对值不等式的解法,涉及一元一次不等式的解法,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
16.已知函数y=lgx的定义域为集合A,集合B={0,1,2},则A∩B=( )
| A. | (0,+∞) | B. | (0,2] | C. | {0,1,2} | D. | {1,2} |
 中,
中, 是
是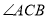 的角平分线,
的角平分线,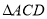 的外接圆交
的外接圆交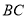 于
于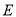 点.
点.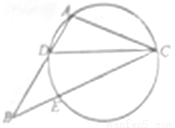
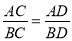 ;
;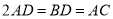 ,求
,求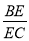 的值.
的值.