题目内容
6.关于x的方程$\frac{1}{||x-1|-1|}$=|sin$\frac{1}{2}$πx|在[-6,6]上解的个数是11.分析 化简y=||x-1|-1|=$\left\{\begin{array}{l}{-\frac{1}{x},x<0}\\{\frac{1}{x},0<x≤1}\\{\frac{1}{2-x},1<x<2}\\{\frac{1}{x-2},x>2}\end{array}\right.$,从而作函数y=$\frac{1}{||x-1|-1|}$与y=|sin$\frac{1}{2}$πx|在[-6,6]上的图象,从而解得.
解答 解:y=||x-1|-1|=$\left\{\begin{array}{l}{-\frac{1}{x},x<0}\\{\frac{1}{x},0<x≤1}\\{\frac{1}{2-x},1<x<2}\\{\frac{1}{x-2},x>2}\end{array}\right.$,
作函数y=$\frac{1}{||x-1|-1|}$与y=|sin$\frac{1}{2}$πx|在[-6,6]上的图象如下,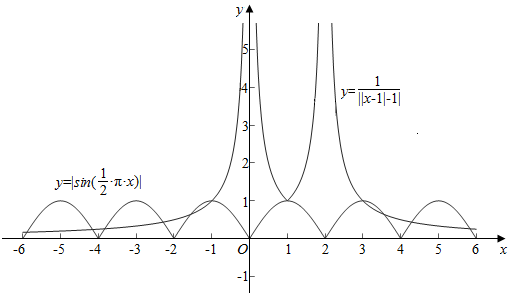
结合图象可知,
两个图象共有11个交点,
故答案为:11.
点评 本题考查了数形结合的思想方法应用及方程与函数的关系应用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
11.函数F(x)=${∫}_{0}^{x}$(t2+2t-8)dt(x>0)的递增区间为( )
| A. | (2,+∞) | B. | (0,2) | C. | (-4,+∞) | D. | (-∞,-4) |
18.5555-1除以8的余数是( )
| A. | 6 | B. | 7 | C. | 1 | D. | 2 |
10.复数$\frac{2-i}{1+{i}^{5}}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |