5555-1除以8的余数是( )A．6B．7C．1D．2 题目和参考答案——青夏教育精英家教网——

题目内容

18．55⁵⁵-1除以8的余数是（　　）

A．

6

B．

7

C．

1

D．

2

分析根据55⁵⁵-1=（56-1）⁵⁵-1，利用二项式定理展开，可得55⁵⁵-1除以8的余数．

解答解：55⁵⁵-1=（56-1）⁵⁵-1=${C}_{55}^{0}$•56⁵⁵-${C}_{55}^{1}$•56⁵⁴+${C}_{55}^{2}$•56⁵³+…+${C}_{55}^{54}$•56+${C}_{55}^{55}$（-1）-1，
除了最后两项外，其余的各项都能被8整除，
故55⁵⁵-1除以8的余数是-2，即55⁵⁵-1除以8的余数是6，
故选：A．

点评本题主要考查利用二项式定理证明整除性，属于基础题．

练习册系列答案

优等生数学系列答案

小学课堂作业系列答案

口算练习册系列答案

金博士一点全通系列答案

课时作业本吉林人民出版社系列答案

天天向上中考零距离教材新解系列答案

阳光互动绿色成长空间系列答案

星火英语Spark巅峰训练系列答案

名师点津随堂小测系列答案

好帮手阅读成长系列答案

相关题目

8．已知$\overrightarrow{i}$、$\overrightarrow{j}$均为单位向量，且互相垂直，若向量$\overrightarrow{a}$=3$\overrightarrow{i}$+2$\overrightarrow{j}$，$\overrightarrow{b}$=-$\overrightarrow{j}$，求向量2$\overrightarrow{b}$-$\overrightarrow{a}$的模．

9．若函教f（x）=log₂（x²-ax+6）在（-∞，2]是减函数，则实数a的取值范围是（　　）

6．关于x的方程$\frac{1}{||x-1|-1|}$=|sin$\frac{1}{2}$πx|在[-6，6]上解的个数是11．

13．已知450°＜α＜510°，则$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cos2α}}$的值是（　　）

-sin$\frac{α}{2}$

cos$\frac{α}{2}$

sin$\frac{α}{2}$

-cos$\frac{α}{2}$

3．与向量$\overrightarrow{a}$=（6，8）共线的单位向量是（　　）

（-$\frac{3}{5}$，-$\frac{4}{5}$）

（$\frac{4}{5}$，$\frac{3}{5}$）

5．已知函数$f（x）=lnx+\frac{2a}{x+1}$，a∈R．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）如果当x＞0，且x≠1时，$\frac{lnx}{x-1}＞\frac{a}{x+1}$恒成立，求实数a的范围．

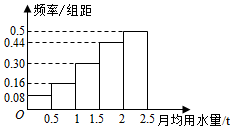如图为某小区100为居民2015年月平均用水量（单位：t）的频率分布直方图的一部分，据此可求这100位居民月平均用水量的中位数为2.02吨．

3．已知cos（α+$\frac{π}{2}$）=$\frac{1}{3}$，则cos2α的值等于（　　）