题目内容
数列3、5、9、17、33…的一个通项公式是an= ．
考点：数列的概念及简单表示法
专题：等差数列与等比数列
分析：由数列3、5、9、17、33…可得：a1=2+1，a2=22+1，a3=23+1，…，即可得出．
解答：
解：由数列3、5、9、17、33…可得：
a1=2+1，a2=22+1，a3=23+1，…，
可得：an=2n+1．
故答案为：2n+1．
a1=2+1，a2=22+1，a3=23+1，…，
可得：an=2n+1．
故答案为：2n+1．
点评：本题考查了通过观察分析猜想归纳求数列的通项公式，注意2n的应用，属于基础题．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
函数y=x2-4x+6，x∈[1，5）的值域为（ ）
| A、[2，+∞） |
| B、（-∞，2] |
| C、[2，11] |
| D、[2，11） |
已知函数f（x）在区间[-5，5]上是奇函数，在区间[0，5]上是单调函数，且f（3）＜f（1），则（ ）
| A、f（-1）＜f（-3） |
| B、f（0）＞f（-1） |
| C、f（-1）＜f（1） |
| D、f（-3）＞f（-5） |
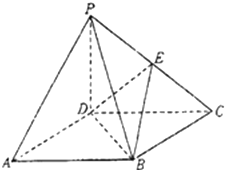如图，四棱锥P-ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．若集合A={0，1，2，3，4}，B={1，2，4}则A∪B=（ ）
| A、{0，1，2，3，4} |
| B、{1，2，3，4} |
| C、{1，2} |
| D、{0} |