题目内容
7.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按31天算,记该女子一个月中的第n天所织布的尺数为an,则$\frac{{{a_1}+{a_3}+…+{a_{29}}+{a_{31}}}}{{{a_2}+{a_4}+…+{a_{28}}+{a_{30}}}}$的值为( )| A. | $\frac{16}{5}$ | B. | $\frac{16}{15}$ | C. | $\frac{16}{29}$ | D. | $\frac{16}{31}$ |
分析 由题意可得:每天织布的量组成了等差数列{an},设公差为d(尺),运用等差数列的通项公式和的求和公式即可得出.
解答 解:由题意可得:每天织布的量组成了等差数列{an},
a1=5(尺),S31=9×40+30=390(尺),设公差为d(尺),
则31×5+$\frac{31×30}{2}$d=390,解得d=$\frac{47}{93}$.
则$\frac{{{a_1}+{a_3}+…+{a_{29}}+{a_{31}}}}{{{a_2}+{a_4}+…+{a_{28}}+{a_{30}}}}$=$\frac{16{a}_{1}+\frac{1}{2}×16×15×2d}{15{a}_{2}+\frac{1}{2}×15×14×2d}$
=$\frac{16}{15}$•$\frac{{a}_{1}+15d}{{a}_{2}+14d}$=$\frac{16}{15}$•$\frac{{a}_{16}}{{a}_{16}}$=$\frac{16}{15}$.
故选:B.
点评 本题考查等差数列在实际问题中的运用,考查等差数列的通项公式和求和公式的运用,以及运算能力,属于中档题.

练习册系列答案
相关题目
18.函数f(x)=x3+x2+5ax-1存在极值点的充要条件是( )
| A. | a$≤\frac{1}{15}$ | B. | a<$\frac{1}{15}$ | C. | a$≥\frac{1}{15}$ | D. | a>$\frac{1}{15}$ |
15.已知点P(x0,y0)是抛物线y2=4x上的一个动点,Q是圆C:(x+2)2+(y-4)2=1上的一个动点,则x0+|PQ|的最小值为( )
| A. | $2\sqrt{5}-1$ | B. | $2\sqrt{5}$ | C. | 3 | D. | 4 |
16.要得到函数$y=\frac{1}{2}cos2x$的图象,只需将函数$y=\frac{1}{2}sin2x$的图象( )
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
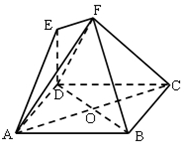 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.