题目内容
已知∠α的顶点在坐标原点O,始边与x轴的非负半轴重合,点P在α的终边上,点Q(-3,-4)且tanα=-2,则
与
的夹角的余弦值为( )
| OP |
| OQ |
A、-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由题意可得
=(-3,-4),由三角函数定义和向量的关系可得
=(-
,
)或(
,-
),由夹角公式可求.
| OQ |
| OP |
| 1 | ||
|
| 2 | ||
|
| 1 | ||
|
| 2 | ||
|
解答:
解:由题意可得
=(-3,-4),
又∵tanα=-2,
∴α的终边与单位圆的交点为(-
,
)或(
,-
)
∴可取
=(-
,
)或(
,-
)
当
=(-
,
)时,由夹角公式可得
与
的夹角的余弦值cosθ=
=-
;
当
=(
,-
)时,由夹角公式可得
与
的夹角的余弦值cosθ=
=
;
故选:C
| OQ |
又∵tanα=-2,
∴α的终边与单位圆的交点为(-
| 1 | ||
|
| 2 | ||
|
| 1 | ||
|
| 2 | ||
|
∴可取
| OP |
| 1 | ||
|
| 2 | ||
|
| 1 | ||
|
| 2 | ||
|
当
| OP |
| 1 | ||
|
| 2 | ||
|
| OP |
| OQ |
| ||||
|
|
| ||
| 5 |
当
| OP |
| 1 | ||
|
| 2 | ||
|
| OP |
| OQ |
| ||||
|
|
| ||
| 5 |
故选:C
点评:本题考查数量积与向量的夹角,涉及三角函数的运算和分类思想,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知椭圆C:
已知椭圆C: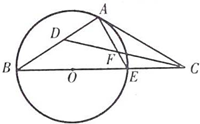 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点.F
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点.F