题目内容
已知椭圆C与双曲线x2-
=1的焦点相同,且与直线y=x+4有公共点,当椭圆C的长轴最短时,椭圆C的离心率= .
| y2 |
| 3 |
考点:椭圆的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据已知条件便可得到c=2,并且可设出椭圆C的方程为
+
=1,并且得到方程组
有解,从而得到方程
+
=1有解,所以根据判别式△≥0得到a2≥10,所以a的最小值为
,所以带入椭圆的离心率公式即可求其离心率.
| x2 |
| a2 |
| y2 |
| a2-4 |
|
| x2 |
| a2 |
| (x+4)2 |
| a2-4 |
| 10 |
解答:
解:椭圆C的焦点为(-2,0),(2,0);
∴设椭圆的方程为
+
=1;
椭圆C与直线y=x+4有公共点;
∴方程
+
=1,即(
+
)x2+
x+
-1=0有解;
∴△=a4-14a2+40≥0;
解得a2≥10,或a2≤4;
∵a>2;
∴a2≥10;
∴a的最小值为
;
∴该椭圆的离心率为
=
=
.
故答案为:
.
∴设椭圆的方程为
| x2 |
| a2 |
| y2 |
| a2-4 |
椭圆C与直线y=x+4有公共点;
∴方程
| x2 |
| a2 |
| (x+4)2 |
| a2-4 |
| 1 |
| a2 |
| 1 |
| a2-4 |
| 8 |
| a2-4 |
| 16 |
| a2-4 |
∴△=a4-14a2+40≥0;
解得a2≥10,或a2≤4;
∵a>2;
∴a2≥10;
∴a的最小值为
| 10 |
∴该椭圆的离心率为
| c |
| a |
| 2 | ||
|
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:考查双曲线、椭圆的标准方程,椭圆的长轴、焦点的概念,椭圆与直线有公共点时对应的方程的关系,一元二次方程有解的充要条件,以及椭圆离心率的计算公式.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
在同一平面直角坐标系中,已知函数y=f(x)的图象与y=ex的图象关于直线y=x对称,则函数y=f(x)-x的单调增区间为( )
| A、(-∞,1] |
| B、(0,+∞) |
| C、[1,+∞) |
| D、(0,1] |
已知∠α的顶点在坐标原点O,始边与x轴的非负半轴重合,点P在α的终边上,点Q(-3,-4)且tanα=-2,则
与
的夹角的余弦值为( )
| OP |
| OQ |
A、-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
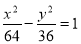 上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________.
上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为________. 写出下列关于角的集合.
写出下列关于角的集合.