题目内容
证明:1•1!+2•2!+…+n•n!=(n+1)!-1.
考点:排列及排列数公式
专题:排列组合
分析:本题属于关于置之死地命题的证明,所以利用数学归纳法矩形证明即可.
解答:
证明:n=1时,左边=1,右边=2!-1=1;
假设n=k等式成立,即1•1!+2•2!+3•3!+k•k!=(k+1)!-1,
则n=k+1时,1•1!+2•2!+3•3!+k•k!+(k+1)•(k+1)!=(k+1)!-1+(k+1)•(k+1)!=(k+1)!(1+k+1)-1=(k+2)!-1;
所以n=k+1时等式成立;
所以1•1!+2•2!+…+n•n!=(n+1)!-1对任意的n∈N成立.
假设n=k等式成立,即1•1!+2•2!+3•3!+k•k!=(k+1)!-1,
则n=k+1时,1•1!+2•2!+3•3!+k•k!+(k+1)•(k+1)!=(k+1)!-1+(k+1)•(k+1)!=(k+1)!(1+k+1)-1=(k+2)!-1;
所以n=k+1时等式成立;
所以1•1!+2•2!+…+n•n!=(n+1)!-1对任意的n∈N成立.
点评:本题考查用数学归纳法证明等式成立,用数学归纳法证明问题的步骤是:第一步验证当n=n0时命题成立,第二步假设当n=k时命题成立,那么再证明当n=k+1时命题也成立.本题解题的关键是利用第二步假设中结论证明当n=k+1时成立,本题是一个中档题目

练习册系列答案
相关题目
在同一平面直角坐标系中,已知函数y=f(x)的图象与y=ex的图象关于直线y=x对称,则函数y=f(x)-x的单调增区间为( )
| A、(-∞,1] |
| B、(0,+∞) |
| C、[1,+∞) |
| D、(0,1] |
已知∠α的顶点在坐标原点O,始边与x轴的非负半轴重合,点P在α的终边上,点Q(-3,-4)且tanα=-2,则
与
的夹角的余弦值为( )
| OP |
| OQ |
A、-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
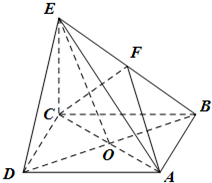 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥平面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥平面ABCD,F为BE的中点.