题目内容
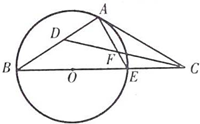如图，点C是圆O的直径BE的延长线上一点，AC是圆O的切线，A为切点，∠ACB的平分线CD与AB相交于点D，与AE相交于点．F（Ⅰ）求∠ADF的度数；（Ⅱ）若AB=AC，求
| AC |
| BC |
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（Ⅰ）利用切线的性质和角平分线的性质可得∠ADF=∠AFD．再利用BE是⊙O直径，可得∠BAE=90°．即可得到∠ADF=45°．
（Ⅱ）利用等边对等角∠B=∠ACB=∠EAC．由（I）得∠BAE=90°，∠B+∠AEB=∠B+∠ACE+∠EAC=3∠B=90°，即可得到∠B=30°．进而得到△ACE∽△BCA，于是
=
=tan30°
（Ⅱ）利用等边对等角∠B=∠ACB=∠EAC．由（I）得∠BAE=90°，∠B+∠AEB=∠B+∠ACE+∠EAC=3∠B=90°，即可得到∠B=30°．进而得到△ACE∽△BCA，于是
| AC |
| BC |
| AE |
| AB |
解答：
解：（Ⅰ）∵AC是⊙O的切线，∴∠B=∠EAC．
又∵DC是∠ACB的平分线，∴∠ACD=∠DCB，
∴∠B+∠DCB=∠EAC+∠ACD，∴∠ADF=∠AFD．
∵BE是⊙O直径，∴∠BAE=90°．
∴∠ADF=45°．
（Ⅱ）∵AB=AC，∴∠B=∠ACB=∠EAC．
由（I）得∠BAE=90°，∴∠B+∠AEB=∠B+∠ACE+∠EAC=3∠B=90°，
∴∠B=30°．
∵∠B=∠EAC，∠ACB=∠ACB，
∴△ACE∽△BCA，
∴
=
=tan30°=
．
又∵DC是∠ACB的平分线，∴∠ACD=∠DCB，
∴∠B+∠DCB=∠EAC+∠ACD，∴∠ADF=∠AFD．
∵BE是⊙O直径，∴∠BAE=90°．
∴∠ADF=45°．
（Ⅱ）∵AB=AC，∴∠B=∠ACB=∠EAC．
由（I）得∠BAE=90°，∴∠B+∠AEB=∠B+∠ACE+∠EAC=3∠B=90°，
∴∠B=30°．
∵∠B=∠EAC，∠ACB=∠ACB，
∴△ACE∽△BCA，
∴
| AC |
| BC |
| AE |
| AB |
| ||
| 3 |
点评：熟练掌握圆的性质、切线的性质和角平分线的性质、弦切角定理、相似三角形的性质等是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知∠α的顶点在坐标原点O，始边与x轴的非负半轴重合，点P在α的终边上，点Q（-3，-4）且tanα=-2，则
与
的夹角的余弦值为（ ）
| OP |
| OQ |
A、-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
写出下列关于角的集合．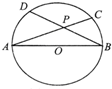
如图，AB是圆O的直径，过A、B的两条弦AC和BD相交于点P，若圆O的半径是3，则AC•AP+BD•BP的值