题目内容
解方程：（5-x）（6-x）（4-x）-4（4-x）-4（6-x）=0．
考点：有理数指数幂的化简求值
专题：计算题
分析：因式分解原方程，转化为一元二次方程求解．
解答：
解：由（5-x）（6-x）（4-x）-4（4-x）-4（6-x）=0，
得：5（6-x）（4-x）-x（6-x）（4-x）-4（4-x）-4（6-x）=0，
∴（4-x）（30-5x-4）-（6-x）（x+4）=0，
即（4-x）（26-5x）-（6-x）（x+4）=0．
整理得：3x2-24x+40=0．
解得：x=
，或x=
．
得：5（6-x）（4-x）-x（6-x）（4-x）-4（4-x）-4（6-x）=0，
∴（4-x）（30-5x-4）-（6-x）（x+4）=0，
即（4-x）（26-5x）-（6-x）（x+4）=0．
整理得：3x2-24x+40=0．
解得：x=
12-2
| ||
| 3 |
12+2
| ||
| 3 |
点评：本题考查了有理指数幂的化简与求值，考查了方程的解法，是基础题．
练习册系列答案
相关题目
已知∠α的顶点在坐标原点O，始边与x轴的非负半轴重合，点P在α的终边上，点Q（-3，-4）且tanα=-2，则
与
的夹角的余弦值为（ ）
| OP |
| OQ |
A、-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
写出下列关于角的集合．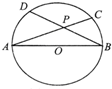
如图，AB是圆O的直径，过A、B的两条弦AC和BD相交于点P，若圆O的半径是3，则AC•AP+BD•BP的值