题目内容
8.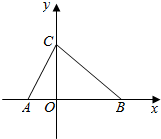 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$(Ⅰ)求△ABC的面积;
(Ⅱ)若函数f(x)=Msin(ωx+φ)(M>0,ω>0),|φ|<$\frac{π}{2}$的图象经过
A、C、B三点,且A、B为f(x)的图象与x轴相邻的两个交点,求f(x)的解析式.
分析 (Ⅰ)由已知及余弦定理可:c2-4c-12=0,解得c的值,利用三角形面积公式即可得解.
(Ⅱ)由(Ⅰ)知,A(-2,0),B(4,0),C(0,2$\sqrt{3}$),又函数f(x)的半个周期$\frac{T}{2}$=6,对称轴为x=1,由周期公式可求T,ω,由$f(1)=Msin(\frac{π}{6}•1+ϕ)=M$,结合范围|φ|<$\frac{π}{2}$可求φ,又$f(0)=Msin\frac{π}{3}=2\sqrt{3}$,即可求得M,从而可求函数f(x)的解析式.
解答 解:(Ⅰ)在△ABC中由余弦定理可知:${a^2}={b^2}+{c^2}-2bccos\frac{π}{3}$,
∴c2-4c-12=0,
∴c=|AB|=6,
∴${S_{△ABC}}=\frac{1}{2}•4•6sin\frac{π}{3}=6\sqrt{3}$.
(Ⅱ) T=2×6=12,
∴$ω=\frac{π}{6}$,
∵$f(1)=Msin(\frac{π}{6}•1+ϕ)=M$,
∴$sin(\frac{π}{6}+φ)=1$,
∴$\frac{π}{6}+φ=2kπ+\frac{π}{2},k∈Z$,
∵$|φ|<\frac{π}{2}$,
∴$φ=\frac{π}{3}$.
又∵$f(0)=Msin\frac{π}{3}=2\sqrt{3}$,
∴M=4,
∴$f(x)=4sin(\frac{π}{6}x+\frac{π}{3})$.
点评 本题考查解三角形和三角函数图象及性质等知识,考查学生运算求解能力、数据处理能力及推理论证能力,考查学生数形结合思想、函数与方程思想及转化与化归思想,属于中档题.

练习册系列答案
相关题目
12.方程(x-1)2+(y+2)2=9表示的图形是( )
| A. | 圆心为(-1,2),半径为3的圆 | B. | 圆心为(-1,2),半径为9的圆 | ||
| C. | 圆心为(1,-2),半径为3的圆 | D. | 圆心为(1,-2),半径为9的圆 |
3.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为5x+2y+1=0,则曲线y=f(x)在点(1,f(1))处的切线的斜率为( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | 2 | D. | -$\frac{1}{2}$ |
18.已知命题p:$\frac{2x}{x-1}$<1,命题q:(x+a)(x-3)<0,若p是q的充分不必要条件,则实数a的取值范围是( )
| A. | (-3,-1] | B. | [-3,-1] | C. | [1,+∞) | D. | (-∞,-3] |



