题目内容
2.已知函数f(x)=$\sqrt{3}$sinωxcosωx-cos2ωx+$\frac{1}{2}$(ω>0),与f(x)图象的对称轴x=$\frac{π}{3}$相邻的f(x)的零点为x=$\frac{π}{12}$.(Ⅰ)讨论函数f(x)在区间$[{-\frac{π}{12},\frac{5π}{12}}]$上的单调性;
(Ⅱ)设△ABC的内角A,B,C的对应边分别为a,b,c,且c=$\sqrt{3}$,f(C)=1,若向量$\overrightarrow m$=(1,sinA)与向量$\overrightarrow n$=(2,sinB)共线,求a,b的值.
分析 (Ⅰ)先确定函数的解析式,再讨论函数f(x)在区间$[{-\frac{π}{12},\frac{5π}{12}}]$上的单调性;
(Ⅱ)求出C,利用$\overrightarrow m=({1,sinA})$与向量$\overrightarrow n=({2,sinB})$共线,所以sinB=2sinA,由正弦定理得,b=2a①,由余弦定理得,c2=a2+b2$-2abcos\frac{π}{3}$,即a2+b2-ab②,即可求a,b的值.
解答 解:(Ⅰ)$f(x)=\frac{{\sqrt{3}}}{2}sin2ωx-\frac{1+cos2ωx}{2}+\frac{1}{2}$=$\frac{{\sqrt{3}}}{2}sin2ωx-\frac{1}{2}cos2ωx$=$sin({2ωx-\frac{π}{6}})$
由与f(x)图象的对称轴$x=\frac{π}{3}$相邻的零点为$x=\frac{π}{12}$,得$\frac{1}{4}•\frac{2π}{2ω}=\frac{π}{3}$$-\frac{π}{12}=\frac{π}{4}$,
所以ω=1,即$f(x)=sin({2x-\frac{π}{6}})$
令$z=2x-\frac{π}{6}$,函数y=sinz单调增区间是$[{-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ}]$,k∈Z,
由$-\frac{π}{2}+2kπ≤2x-$$\frac{π}{6}≤\frac{π}{2}+2kπ$,
得$-\frac{π}{6}+kπ≤x≤\frac{π}{3}+kπ$,k∈Z,
设$A=[{-\frac{π}{12},\frac{5π}{12}}]$,$B=\left\{{\left.x\right|-\frac{π}{6}+kπ≤x≤}\right.$$\left.{\frac{π}{3}+kπ,k∈Z}\right\}$,
易知$A∩B=[{-\frac{π}{12},\frac{π}{3}}]$,
所以当$x∈[{-\frac{π}{12},\frac{5π}{12}}]$时,f(x)在区间$[{-\frac{π}{12},\frac{π}{3}}]$上单调递增,在区间$[{\frac{π}{3},\frac{5π}{12}}]$上单调递减.
(Ⅱ)$f(C)=sin({2C-\frac{π}{6}})-1=0$,则$sin({2C-\frac{π}{6}})=1$,
因为0<C<π,所以$-\frac{π}{6}<2C-\frac{π}{6}<\frac{11π}{6}$,
从而$2C-\frac{π}{6}=\frac{π}{2}$,
解得$C=\frac{π}{3}$.
因为$\overrightarrow m=({1,sinA})$与向量$\overrightarrow n=({2,sinB})$共线,所以sinB=2sinA,
由正弦定理得,b=2a①
由余弦定理得,c2=a2+b2$-2abcos\frac{π}{3}$,即a2+b2-ab②
由①②解得a=1,b=2
点评 本题考查三角函数的图象与性质,考查向量知识的运用,考查正弦、余弦定理的运用,属于中档题.

 考前必练系列答案
考前必练系列答案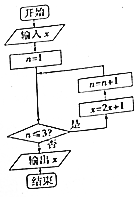 阅读右边程序框图,当输入的值为3时,运行相应程序,则输出x的值为( )
阅读右边程序框图,当输入的值为3时,运行相应程序,则输出x的值为( )| A. | 7 | B. | 15 | C. | 31 | D. | 63 |
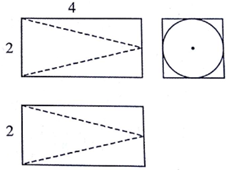
| A. | $16-\frac{2π}{3}$ | B. | $8-\frac{4π}{3}$ | C. | $16-\frac{4π}{3}$ | D. | $16(1-\frac{π}{3})$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | {1,2} | B. | {1,2,4} | C. | {2,4} | D. | {2,3,4} |
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |