题目内容
7.已知集合A={x|log2(x-1)<1},$B=\left\{{x|\frac{x+1}{x-3}<0}\right\}$,则“x∈A”是“x∈B”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用对数函数的单调性化简集合A,利用不等式的解法可得B,再利用简易逻辑的判定方法即可得出.
解答 解:由log2(x-1)<1,可得0<x-1<2,解得1<x<3.
∴A=(1,3).
由$\frac{x+1}{x-3}$<0,?(x+1)(x-3)<0,解得-1<x<3.∴B=(-1,3).
则“x∈A”是“x∈B”的充分不必要条件.
故选:A.
点评 本题考查了对数函数的单调性、不等式的性质与解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
18.若等比数列{an}的公比为q,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=2\\{a_2}x+{a_4}y=1\end{array}\right.$的解的情况下列说法正确的是( )
| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当$q=\frac{1}{2}$时,方程组有无穷多解 | |
| D. | 当且仅当$q=\frac{1}{2}$时,方程组无解 |
16.一个几何体的三视图如图所示,则该几何体的体积为( )
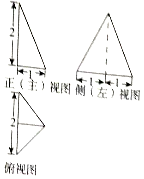

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 3 | D. | $\frac{8}{3}$ |
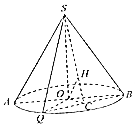 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.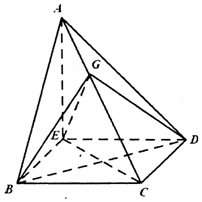 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.