题目内容
1.由曲线y=$\sqrt{x}$,直线y=2-x及y轴所围成的封闭图形的面积为$\frac{5}{6}$.分析 求得交点坐标(1,1),由题意可知:S=${∫}_{0}^{1}$(2-x-$\sqrt{x}$)dx,求得原函数,代入即可求得曲线y=$\sqrt{x}$,直线y=2-x及y轴所围成的封闭图形的面积.
解答 解:由题意$\left\{\begin{array}{l}{y=\sqrt{x}}\\{y=2-x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,交点A(1,1),
曲线y=$\sqrt{x}$,直线y=2-x及y轴所围成的封闭图形的面积S=${∫}_{0}^{1}$(2-x-$\sqrt{x}$)dx=(2x-$\frac{1}{2}$x2-$\frac{2}{3}$${x}^{\frac{3}{2}}$)${丨}_{0}^{1}$=2-$\frac{1}{2}$-$\frac{2}{3}$=$\frac{5}{6}$,
曲线y=$\sqrt{x}$,直线y=2-x及y轴所围成的封闭图形的面积$\frac{5}{6}$,
故答案为:$\frac{5}{6}$.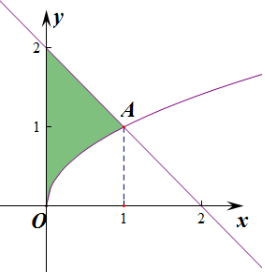
点评 本题考查定积分的应用,考查定积分的运算,考查计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.如表是某商店每月某种商品的销售额(用y表示,单位:万元)与月份(t)的关系对照表.
其中$\overline{y}$=10,$\sum_{i=1}^{5}$tiyi=163.请建立y关于t的回归方程(系数精确到0.01)并预测6月份这种商品的销售额.
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+$\stackrel{∧}{a}$中斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t}({y}_{i}-\overline{y}))}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
| 月份(t) | 1 | 2 | 3 | 4 | 5 |
| 销售额(y) | y1 | y2 | y3 | y4 | y5 |
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+$\stackrel{∧}{a}$中斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t}({y}_{i}-\overline{y}))}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F(-c,0),M、N在双曲线C上,O是坐标原点,若四边形OFMN为平行四边形,且四边形OFMN的面积为$\sqrt{2}$cb,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
9.若不等式mx2+x+n>0的解集是{x|-$\frac{1}{3}$<x<$\frac{1}{2}$},则m,n分别是( )
| A. | 6,-1 | B. | -6,-1 | C. | 6,1 | D. | -6,1 |
16.设函数f(x)=$\left\{{\begin{array}{l}{x-2,x≥10}\\{f[f(x+6)],x<10}\end{array}}$则f(6)=( )
| A. | 10 | B. | -10 | C. | 8 | D. | -8 |
13.直线$\sqrt{3}$x+$\sqrt{3}$y+1=0的倾斜角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
10.函数y=$\frac{\sqrt{x}}{{x}^{2}-1}$的定义域是( )
| A. | {x|x≥0或x≠1} | B. | {x|x≥0或 x≠±1} | C. | {x|x≥且x≠1} | D. | {x|x≥0且x≠1} |
