题目内容
设
=(m+1)
-3
,
=
+(m-1)
,其中
,
为互相垂直的单位向量,又(
+
)⊥(
-
),则实数m= .
| a |
| i |
| j |
| b |
| i |
| j |
| i |
| j |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由(
+
)⊥(
-
),可得(
+
)•(
-
)=
2-
2=0,即可得出.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:∵
=(m+1)
-3
,
=
+(m-1)
,其中
,
为互相垂直的单位向量,
∴
=(m+1,-3),
=(1,m-1).
又(
+
)⊥(
-
),
∴(
+
)•(
-
)=
2-
2=0,
∴(m+1)2+9-[1+(m-1)2]=0,
化为m=-2.
故答案为:-2.
| a |
| i |
| j |
| b |
| i |
| j |
| i |
| j |
∴
| a |
| b |
又(
| a |
| b |
| a |
| b |
∴(
| a |
| b |
| a |
| b |
| a |
| b |
∴(m+1)2+9-[1+(m-1)2]=0,
化为m=-2.
故答案为:-2.
点评:本题考查了向量数量积运算性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
| a |
| x2 |
| 3 |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
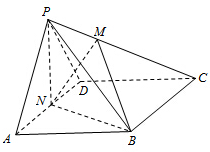 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD