题目内容
14.已知α,β∈(0,π),cosα=$\frac{12}{13}$,cos(α+β)=$\frac{3}{5}$,则cosβ=$\frac{56}{65}$.分析 由已知可得α∈(0,$\frac{π}{2}$),α+β∈(0,$\frac{π}{2}$)或α+β∈($\frac{3π}{2}$,2π),当α+β∈($\frac{3π}{2}$,2π)时,由α∈(0,$\frac{π}{2}$),可得β∈(π,$\frac{3π}{2}$),矛盾,可得α+β∈(0,$\frac{π}{2}$),利用同角三角函数基本关系式可求sinα,sin(α+β),再利用两角差的余弦公式求得cosβ=cos[(α+β)-α]的值.
解答 解:∵α,β∈(0,π),cosα=$\frac{12}{13}$>0,cos(α+β)=$\frac{3}{5}$>0,
∴α∈(0,$\frac{π}{2}$),α+β∈(0,$\frac{π}{2}$)或α+β∈($\frac{3π}{2}$,2π),
∵α+β∈($\frac{3π}{2}$,2π)时,由α∈(0,$\frac{π}{2}$),可得β∈(π,$\frac{3π}{2}$),矛盾,故α+β∈(0,$\frac{π}{2}$),
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{5}{13}$,sin(α+β)=$\sqrt{1-co{s}^{2}(α+β)}$=$\frac{4}{5}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=$\frac{3}{5}$×$\frac{12}{13}$+$\frac{4}{5}×\frac{5}{13}$=$\frac{56}{65}$.
故答案为:$\frac{56}{65}$.
点评 本题主要考查两角和差的余弦公式的应用,同角三角函数的基本关系,体现了分类讨论的数学思想,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | 既不充分也不要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 充分必要条件 |
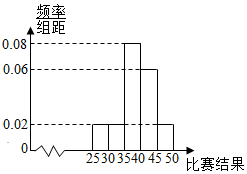 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:| 年龄所在区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
(1)求人数统计表中的a和b的值;
(2)根据频率分布直方图,估计该项比赛结果的中位数;
(3)用分层抽样的方法从第1,2,3组中共抽取6人,再从这6人中随机抽取2人参加上一级比赛活动,求参加上一级比赛活动中至少有1人的比赛结果在第3组的概率.
| A. | [$\frac{5\sqrt{2}}{2}$-1,$\sqrt{34}+1$) | B. | [$\sqrt{17}-1$,$\sqrt{34}+1$] | C. | [$\sqrt{17}$,$\sqrt{34}$] | D. | [$\sqrt{17}$-1,$\sqrt{34}$-1] |
| A. | 4 | B. | 4或-3 | C. | -3或-1 | D. | -3 |