题目内容
17．若f（x）=（$\frac{1}{{e}^{x}-1}$+$\frac{1}{2}$）+x，则函数f（x）的图象是（ ）| A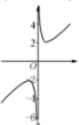． |  | B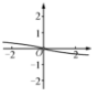． |  | C． |  | D． |  |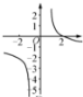
分析 根据函数的值域，单调性判断．
解答 解：由函数有意义得ex-1≠0，即x≠0．排除B．
当x＞0时，ex＞1，∴f（x）=（$\frac{1}{{e}^{x}-1}$+$\frac{1}{2}$）+x＞0，排除D．
当x＜0时，0＜ex＜1，∴$\frac{1}{{e}^{x}-1}$+$\frac{1}{2}$＜-$\frac{1}{2}$．∴f（x）=（$\frac{1}{{e}^{x}-1}$+$\frac{1}{2}$）+x＜0．排除C．
故选：A．
点评 本题考查了函数图象的判断，属于中档题．
练习册系列答案
相关题目
7．将函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到函数f（x）的图象，则f（x）=（ ）
| A． | cos2x | B． | sin（2x+$\frac{π}{4}$） | C． | -cos2x | D． | -sin2x |
12．
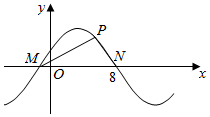如图所示，M，N是函数y=2sin（ωx+ϕ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时，PM⊥PN，则ω=（ ）
如图所示，M，N是函数y=2sin（ωx+ϕ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时，PM⊥PN，则ω=（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | 8 |
2．
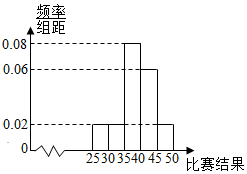为了解我市高三学生参加体育活动的情况，市直属某校高三学生500人参加“体育基本素质技能”比赛活动，按某项比赛结果所在区间分组：第1组：[25，300，第2组：[30，35），第3组：[35，40），第4组：[40，45），第5组：[45，50]，得到不完整的人数统计表如下：
其频率分布直方图为：
（1）求人数统计表中的a和b的值；
（2）根据频率分布直方图，估计该项比赛结果的中位数；
（3）用分层抽样的方法从第1，2，3组中共抽取6人，再从这6人中随机抽取2人参加上一级比赛活动，求参加上一级比赛活动中至少有1人的比赛结果在第3组的概率．
为了解我市高三学生参加体育活动的情况，市直属某校高三学生500人参加“体育基本素质技能”比赛活动，按某项比赛结果所在区间分组：第1组：[25，300，第2组：[30，35），第3组：[35，40），第4组：[40，45），第5组：[45，50]，得到不完整的人数统计表如下：| 年龄所在区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
| 人数 | 50 | 50 | a | 150 | b |
（1）求人数统计表中的a和b的值；
（2）根据频率分布直方图，估计该项比赛结果的中位数；
（3）用分层抽样的方法从第1，2，3组中共抽取6人，再从这6人中随机抽取2人参加上一级比赛活动，求参加上一级比赛活动中至少有1人的比赛结果在第3组的概率．
6．设D为不等式组$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 2x+y-3≤0\end{array}\right.$表示的平面区域，圆C：（x-5）2+y2=1上的点与区域D上的点之间的距离的取值范围是（ ）
| A． | [$\frac{5\sqrt{2}}{2}$-1，$\sqrt{34}+1$） | B． | [$\sqrt{17}-1$，$\sqrt{34}+1$] | C． | [$\sqrt{17}$，$\sqrt{34}$] | D． | [$\sqrt{17}$-1，$\sqrt{34}$-1] |
