题目内容
20．函数f（x）=$\frac{1}{ln|x|}$的图象大致为（ ）| A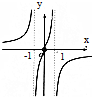． |  | B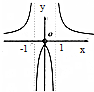． |  | C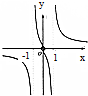． |  | D． |  |
分析 根据函数的奇偶性和特殊值进行判断．
解答 解：∵f（-x）=$\frac{1}{ln|-x|}=\frac{1}{ln|x|}=f（x）$，
∴f（x）是偶函数，即f（x）的图象关于y轴对称．排除A，C．
当x＞1时，f（x）=ln|x|=lnx＞0，排除D．
故选：B．
点评 本题考查了对数函数的性质，函数图象的判断，使用排除法可快速判断出答案．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图．
已知抛物线C：x2=4y，F为抛物线焦点，圆E：x2+（y+1）2=1，斜率为k（k＞0）的直线l与抛物线C和圆E都相切，切点分别为P和Q，直线PF和PQ分别交x轴于点M，N．
12．
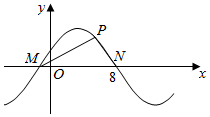如图所示，M，N是函数y=2sin（ωx+ϕ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时，PM⊥PN，则ω=（ ）
如图所示，M，N是函数y=2sin（ωx+ϕ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时，PM⊥PN，则ω=（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | 8 |