题目内容
10.以双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F为圆心,a为半径的圆恰好与双曲线的两条渐近线相切,则该双曲线的离心率为$\sqrt{2}$.分析 根据圆和渐近线的垂直关系建立方程条件进行求解即可.
解答 解:由题意知圆心F(c,0),双曲线的渐近线为y=±$\frac{b}{a}$x,不妨设其中一条为bx-ay=0,
∵圆与渐近线相切,
∴圆心到渐近线的距离d=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{bc}{c}$=b=a,
即c=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{2}a$
即离心率e=$\frac{c}{a}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题主要考查双曲线离心率的计算,根据直线和圆的相切关系建立方程是解决本题的关键.

练习册系列答案
相关题目
20.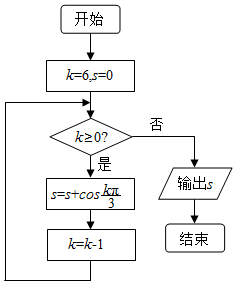 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )
 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
5.下列命题是真命题是( )
| A. | ?x∈R,使得|x|≤0成立 | B. | ¬p为真,则p∨q一定是假 | ||
| C. | x-y=0成立的充要条件是$\frac{x}{y}$=1 | D. | ?x∈R,都有ex>xe |
19.各项均不为零的等差数列{an}中,若an+1=an2-an-1(n∈N*,n≥2),则S2016=( )
| A. | 0 | B. | 2 | C. | 2015 | D. | 4032 |