题目内容
16.已知函数y=Asin(ωx+φ)(ω>0,-π≤φ<π)的图象如图所示,则φ的值为(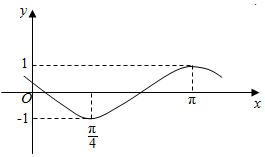
| A. | 0 | B. | -$\frac{5π}{6}$ | C. | $\frac{5π}{6}$ | D. | -$\frac{π}{6}$ |
分析 由图可求T,从而利用周期公式可求得ω,又函数经过(π,1),结合范围-π≤φ<π可求得φ.
解答 解:∵由图可得:T=2×($π-\frac{π}{4}$)=$\frac{3π}{2}$=$\frac{2π}{|ω|}$,ω>0,
∴解得ω=$\frac{4}{3}$;
又∵函数经过(π,1),
∴$\frac{4}{3}$π+φ=2kπ+$\frac{π}{2}$,k∈Z.
∴φ=2kπ-$\frac{5π}{6}$,k∈Z.
又∵-π≤φ<π,
∴可得:φ=-$\frac{5π}{6}$.
故选:B.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得φ是关键,也是难点,考查识图与运算能力,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
11.已知全集U=R,A=$\left\{{x\left|{\left.{\frac{x+1}{2-x}≥0}\right\}}\right.}$,B={x|lnx<0},则A∪B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|x<-1或x≥2} | D. | {x|0<x<2} |
8.已知抛物线C:y2=2px(p>0)的焦点F到双曲线$\frac{x^2}{3}$-y2=1的渐近线的距离为l,过焦点F且斜率为k的直线与抛物线C交于A,B两点,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,则|k|=( )
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $2\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{3}$ |
5.下列命题是真命题是( )
| A. | ?x∈R,使得|x|≤0成立 | B. | ¬p为真,则p∨q一定是假 | ||
| C. | x-y=0成立的充要条件是$\frac{x}{y}$=1 | D. | ?x∈R,都有ex>xe |



