题目内容
15.已知函数f(x)=$\sqrt{3}$sin2x-2cos2x-a在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上的最大值为2.(1)求函数f(x)在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上的值域;
(2)设$α,β∈({0,\frac{π}{2}}),f({\frac{1}{2}α+\frac{π}{12}})=\frac{10}{13},f({\frac{1}{2}β+\frac{π}{3}})=\frac{6}{5}$,求sin(α-β)的值.
分析 (1)f(x)=$\sqrt{3}$sin2x-2cos2x-a=2sin(2x-$\frac{π}{6}$)-a-1,利用函数f(x)=$\sqrt{3}$sin2x-2cos2x-a在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上的最大值为2,求出a,即可求函数f(x)在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上的值域;
(2)设$α,β∈({0,\frac{π}{2}}),f({\frac{1}{2}α+\frac{π}{12}})=\frac{10}{13},f({\frac{1}{2}β+\frac{π}{3}})=\frac{6}{5}$,求出sinα=$\frac{5}{13}$,cosα=$\frac{12}{13}$,cosβ=$\frac{3}{5}$,sinβ=$\frac{4}{5}$,即可求sin(α-β)的值.
解答 解:(1)f(x)=$\sqrt{3}$sin2x-2cos2x-a=2sin(2x-$\frac{π}{6}$)-a-1.
∵x∈[-$\frac{π}{12}$,$\frac{π}{2}$],∴2x-$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{5π}{6}$]
∴当2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$时,f(x)取最大值2,即有2-a-1=2,得a=-1.
∴f(x)=2sin(2x-$\frac{π}{6}$),
则当2x-$\frac{π}{6}$=-$\frac{π}{3}$,即x=-$\frac{π}{12}$时,f(x)取最小值-$\sqrt{3}$,
∴函数f(x)在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上的值域为[-$\sqrt{3}$,2];
(2)∵$α,β∈({0,\frac{π}{2}}),f({\frac{1}{2}α+\frac{π}{12}})=\frac{10}{13},f({\frac{1}{2}β+\frac{π}{3}})=\frac{6}{5}$,
∴sinα=$\frac{5}{13}$,cosα=$\frac{12}{13}$,cosβ=$\frac{3}{5}$,sinβ=$\frac{4}{5}$,
∴sin(α-β)=sinαcosβ-cosαsinβ=-$\frac{33}{65}$.
点评 本题考查三角函数的图象与性质,考查三角函数的化简,考查学生的计算能力,属于中档题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
| A. | {x|2≤x≤3} | B. | {x|-2≤x≤3} | C. | {x|-2≤x<2} | D. | {x|-4<x≤3} |
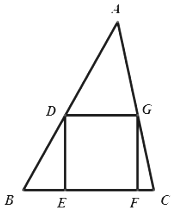 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,