题目内容
8.设函数$f(x)=2x+\frac{1}{x}-1(x>0)$,则f(x)( )| A. | 有最小值 | B. | 有最大值 | C. | 是增函数 | D. | 是减函数 |
分析 利用基本不等式的性质即可得出.
解答 解:∵x>0,
∴函数f(x)=2x+$\frac{1}{x}$-1≥2$\sqrt{2x•\frac{1}{x}}$-1=2$\sqrt{2}$-1,当且仅当x=$\frac{\sqrt{2}}{2}$时取等号,
∴f(x)有最小值,无最大值,
故选:A
点评 本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
16.已知a=log30.2,b=30.2,c=0.30.2,则a,b,c三者的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
20.△ABC中,若sin(A+B)sin(A-B)=sin2C,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
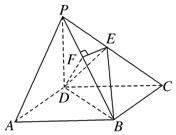 如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.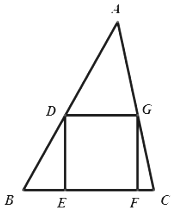 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,