题目内容
16.已知曲线C的极坐标方程为${ρ^2}=\frac{9}{{{{cos}^2}θ+9{{sin}^2}θ}}$,以极点为平面直角坐标系的原点,极轴为x轴的正半轴建立平面直角坐标系.(1)求曲线C的普通方程;
(2)A、B为曲线C上两个点,若OA⊥OB,求$\frac{1}{{|OA{|^2}}}+\frac{1}{{|OB{|^2}}}$的值.
分析 (1)由${ρ^2}=\frac{9}{{{{cos}^2}θ+9{{sin}^2}θ}}$,得ρ2cos2θ+9ρ2sin2θ=9,将x=ρcosθ,y=ρsinθ代入,能求出曲线C的普通方程.
(2)由${ρ^2}=\frac{9}{{{{cos}^2}θ+9{{sin}^2}θ}}$,得$\frac{1}{ρ^2}=\frac{{{{cos}^2}θ}}{9}+{sin^2}θ$,由OA⊥OB,设A(ρ1,α),则B点的坐标可设为$({ρ_2},α±\frac{π}{2})$,由此能求出$\frac{1}{{|OA{|^2}}}+\frac{1}{{|OB{|^2}}}$的值.
解答 解:(1)由${ρ^2}=\frac{9}{{{{cos}^2}θ+9{{sin}^2}θ}}$,得ρ2cos2θ+9ρ2sin2θ=9,
将x=ρcosθ,y=ρsinθ代入,
得到曲线C的普通方程是$\frac{x^2}{9}+{y^2}=1$. …(5分)
(2)因为${ρ^2}=\frac{9}{{{{cos}^2}θ+9{{sin}^2}θ}}$,
所以$\frac{1}{ρ^2}=\frac{{{{cos}^2}θ}}{9}+{sin^2}θ$,
由OA⊥OB,设A(ρ1,α),则B点的坐标可设为$({ρ_2},α±\frac{π}{2})$,
所以$\frac{1}{{|OA{|^2}}}+\frac{1}{{|OB{|^2}}}$=$\frac{1}{ρ_1^2}+\frac{1}{ρ_2^2}$=$\frac{{{{cos}^2}α}}{9}+{sin^2}α$$+\frac{{{{sin}^2}α}}{9}+{cos^2}α$=$\frac{1}{9}+1=\frac{10}{9}$. …(10分)
点评 本题考查曲线的普通方程的求法,考查两线段平方的倒数和的求法,是中档题,解题时要认真审题,极坐标方程、直角坐标方程互化合理运用.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | {x|2≤x≤3} | B. | {x|-2≤x≤3} | C. | {x|-2≤x<2} | D. | {x|-4<x≤3} |
| A. | (-∞,1) | B. | (-∞,1] | C. | (1,+∞) | D. | [1,+∞) |
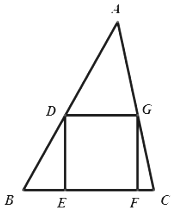 如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,