Question

一个圆锥过轴的截面为等边三角形，它的顶点和底面圆周在球O的球面上，则该圆锥的表面积与球O的表面积的比值为（　　）

• A、

  3

  7

• B、

  9

  25

• C、

  3

  16

• D、

  9

  16

Answer 1

考点：球的体积和表面积

专题：计算题,球

分析：设出球的半径，求出圆锥的底面半径然后求出球的面积以及圆锥的全面积，即可求出结果．

解答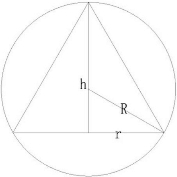： 解：如图，设球半径为R，则锥的底面半径 r=

3

2

R，锥的高 h=

3

2

R．
∴S_锥=S_底面积+S_侧=πr² +πRr=π （

3

2

R）²+

1

2

×

3

2

R•

3

Rπ=

9π

4

R²
S_球=4πR²．
S_锥：S_球=

9π 4 R2

4πR2

=

9

16

，
故选：D．

点评：本题考查球的内接体，圆锥的表面积以及球的面积的求法，考查计算能力．