题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(-x),x<0}\\{1+{2}^{x},x>0}\end{array}\right.$,则f(f(-3))等于( )| A. | -3 | B. | 2 | C. | -2 | D. | 4 |
分析 先求出f(-3)=log23,从而f(f(-3))=f(log23),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(-x),x<0}\\{1+{2}^{x},x>0}\end{array}\right.$,
∴f(-3)=log23,
∴f(f(-3))=f(log23)=1+${2}^{lo{g}_{2}3}$=1+3=4.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
10.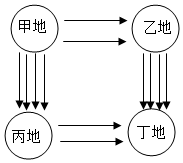 如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )
如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )
 如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )
如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )| A. | 11条 | B. | 14条 | C. | 16条 | D. | 48条 |
14.计算1!+2!+3!+…+100!得到的数,其个位数字是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 定义域是
定义域是 ,则
,则 的定义域( )
的定义域( ) B.
B.
 D.
D.
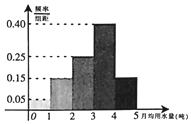 为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.
为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.