题目内容
11.在区间(0,+∞)上,函数y=lg(1+$\frac{1}{x}$)是( )| A. | 增函数,且y>0 | B. | 增函数,且y<0 | C. | 减函数,且y>0 | D. | 减函数,且y<0 |
分析 根据x∈(0,+∞)判断1+$\frac{1}{x}$∈(1,+∞),即lg(1+$\frac{1}{x}$)>0;再判定函数y=lg(1+$\frac{1}{x}$)是单调减函数即可.
解答 解:x∈(0,+∞)时,$\frac{1}{x}$∈(0,+∞),
∴1+$\frac{1}{x}$∈(1,+∞),
∴lg(1+$\frac{1}{x}$)>0,
即y>0;
又t=$\frac{1}{x}$是区间(0,+∞)上的单调减函数,
∴函数y=lg(1+$\frac{1}{x}$)在区间(0,+∞)上是单调减函数,且y>0.
故选:C.
点评 本题考查了对数函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
17.已知$α∈(-\frac{π}{2},0)$且$sin(\frac{π}{2}+α)=\frac{4}{5}$,则tanα=( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
18.如图,在梯形ABCD中,AB=3CD,则下列判断正确的是( )
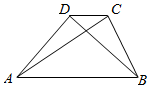

| A. | $\overrightarrow{AB}$=3$\overrightarrow{CD}$ | B. | $\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ | C. | $\overrightarrow{BD}$=$\overrightarrow{AB}$-$\overrightarrow{AD}$ | D. | $\overrightarrow{BC}$=-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ |