题目内容
16.已知f(x)=x3-$\frac{9}{2}$x2+6x+a,若?x0∈[1,4],使f(x0)=2a成立,则a的范围是[2,16].分析 利用导数求出f(x)在x∈[1,4]上的最大与最小值,由f(x0)=2a得出不等式组$\left\{\begin{array}{l}{2+a≤2a}\\{2a≤16+a}\end{array}\right.$,求出解集即可.
解答 解:∵f(x)=x3-$\frac{9}{2}$x2+6x+a,
∴f′(x)=3x2-9x+6=3(x-1)(x-2),
令f′(x)>0,解得x∈(-∞,1)∪(2,+∞);
∴函数f(x)的单调增区间为(-∞,1)和(2,+∞);
令f′(x)<0,解得x∈(1,2),
∴函数f(x)的单调减区间为(1,2);
又x∈[1,4],∴f(x)在(1,2)上是单调减函数,在(2,4)上是单调增函数;
∴f(x)在[1,4]上的最小值为f(2)=8-$\frac{9}{2}$×4+12+a=2+a,最大值为max{f(1),f(4)}=16+a;
又?x0∈[1,4],使f(x0)=2a成立,
∴$\left\{\begin{array}{l}{2+a≤2a}\\{2a≤16+a}\end{array}\right.$,解得2≤a≤16.
∴a的范围是[2,16].
故答案为:[2,16].
点评 本题考查了利用导数求出函数在闭区间上的最值问题,也考查了转化思想的应用问题,是综合性题目.

练习册系列答案
相关题目
11.在区间(0,+∞)上,函数y=lg(1+$\frac{1}{x}$)是( )
| A. | 增函数,且y>0 | B. | 增函数,且y<0 | C. | 减函数,且y>0 | D. | 减函数,且y<0 |
3.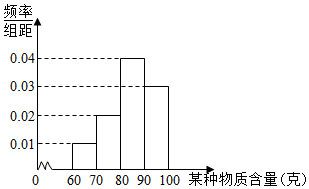 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
(I)估计产品中该物质含量的平均数及方差(同一组数据用该区间的中点值作代表);
(Ⅱ)规定产品的级别如表:
现质检部门从三个等级的产品中采用分层抽样的方式抽取10件产品,再从中随机抽取3件产品进行检测,记质检部门“抽到B或C级品的个数为ξ”,求ξ的分布列和数学期望.
 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.(I)估计产品中该物质含量的平均数及方差(同一组数据用该区间的中点值作代表);
(Ⅱ)规定产品的级别如表:
| 产品级别 | C | B | A |
| 某押麴质含量范围 | [60,70) | [70,80) | [80,100] |