题目内容
17.已知$α∈(-\frac{π}{2},0)$且$sin(\frac{π}{2}+α)=\frac{4}{5}$,则tanα=( )| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
分析 由已知利用诱导公式求得cosα,再由同角三角函数的基本关系式求得答案.
解答 解:由$sin(\frac{π}{2}+α)=\frac{4}{5}$,得cosα=$\frac{4}{5}$,
由$α∈(-\frac{π}{2},0)$,∴sin$α=-\sqrt{1-co{s}^{2}α}$=$-\sqrt{1-(\frac{4}{5})^{2}}=-\frac{3}{5}$,
∴tan$α=\frac{sinα}{cosα}=\frac{-\frac{3}{5}}{\frac{4}{5}}=-\frac{3}{4}$.
故选:A.
点评 本题考查利用诱导公式化简求值,关键是熟记三角函数的象限符号,是基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
11.在区间(0,+∞)上,函数y=lg(1+$\frac{1}{x}$)是( )
| A. | 增函数,且y>0 | B. | 增函数,且y<0 | C. | 减函数,且y>0 | D. | 减函数,且y<0 |
9.奇函数f(x),当x<0时,有f(x)=x(2-x),则f(4)的值为( )
| A. | 12 | B. | -12 | C. | -24 | D. | 24 |
6.由两个1,两个2,两个3组成的6位数的个数为( )
| A. | 45 | B. | 90 | C. | 120 | D. | 360 |
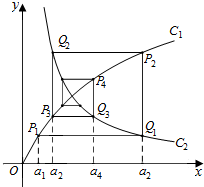 如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}
如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}