题目内容
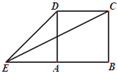 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=考点:正弦定理,二倍角的余弦
专题:三角函数的求值
分析:由正方形边长与AE相等,得到三角形AED为等腰直角三角形,确定出∠EDC=135°,再直角三角形BCE中,利用勾股定理求出CE的长,在三角形CDE中,利用正弦定理求出sin∠CED的值,所求式子利用二倍角的余弦函数公式化简,把sin∠CED的值代入计算即可求出值.
解答:
解:∵四边形ABCD为正方形,且边长为1,
∴∠B=∠ADC=90°,AB=BC=CD=AD=AE=1,
∴△AED为等腰直角三角形,
∴∠AED=∠ADE=45°,
∴∠EDC=135°,
在Rt△BCE中,根据勾股定理得:EC=
=
=
,
在△DEC中,利用正弦定理得:
=
,即
=
,
∴sin∠CED=
,
则cos2∠CED=1-2sin2∠CED=
.
故答案为:
.
∴∠B=∠ADC=90°,AB=BC=CD=AD=AE=1,
∴△AED为等腰直角三角形,
∴∠AED=∠ADE=45°,
∴∠EDC=135°,
在Rt△BCE中,根据勾股定理得:EC=
| EB2+BC2 |
| 22+12 |
| 5 |
在△DEC中,利用正弦定理得:
| EC |
| sin∠EDC |
| DC |
| sin∠CED |
| ||
| sin135° |
| 1 |
| sin∠CED |
∴sin∠CED=
| ||
| 10 |
则cos2∠CED=1-2sin2∠CED=
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题考查了二倍角的余弦函数公式,正方形的性质,等腰直角三角形的性质,以及正弦定理,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
已知等比数列{an},a4+a8=∫
dx,则a6(a2+2a6+a10)的值为( )
2 0 |
| 4-x2 |
| A、π2 | B、π |
| C、4 | D、-9π |