题目内容
已知f(x)=(x2+1)ex,经过点P(0,t)(t≠1)有且只有一条直线与曲线f(x)相切,则t的取值范围是 .
考点:利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:因为f(0)=1则P不在曲线上,设出直线与曲线的切点坐标,则当x=m时导函数的值为切线的斜率,切线过P点,表示出切线方程,利用导数研究g(x)的单调性并得到g(x)的最值,利用直线y=t与曲线g(x)=ex(-x3-x2-x+1)有且只有一个交点得到t的取值范围.
解答:
 解:因为f(x)=(x2+1)ex,f′(x)=ex(x+1)2
解:因为f(x)=(x2+1)ex,f′(x)=ex(x+1)2
因为f(0)=1,所以点P(0,t)不在曲线f(x)上,设过点P的直线与曲线f(x)相切与点A(m,n),
则切线方程为y=em(m+1)2x+t,
所以有n=em(m+1)2m+t及n=em(m2+1),得t=em(-m3-m2-m+1)令g(x)=ex(-x3-x2-x+1),
则g′(x)=ex(-x3-x2-x+1)+ex(-3x2-2x-1)=-x(x+1)(x+3)ex,
令g′(x)=0,得x1=-3,x2=-1,x3=0,
可得g(x)在区间(-∞,-3),(-1,0)单调递增,在区间(-3,-1)(0,+∞)单调递减,
所以g(x)在x=-3时取极大值g(-3)=
,在x=-1时取极小值g(-1)=
,在x=0时取极大值g(0)=1,
又
>1,所以g(-3)=
是g(x)的最大值,
如图,过点P(0,t)有且只有一条直线与曲线f(x)相切等价于直线y=t与曲线g(x)=ex(-x3-x2-x+1)有且只有一个交点,又当x<-3时,g(x)>0,
所以t=
或t≤0.
故答案为:t=
或t≤0.
 解:因为f(x)=(x2+1)ex,f′(x)=ex(x+1)2
解:因为f(x)=(x2+1)ex,f′(x)=ex(x+1)2因为f(0)=1,所以点P(0,t)不在曲线f(x)上,设过点P的直线与曲线f(x)相切与点A(m,n),
则切线方程为y=em(m+1)2x+t,
所以有n=em(m+1)2m+t及n=em(m2+1),得t=em(-m3-m2-m+1)令g(x)=ex(-x3-x2-x+1),
则g′(x)=ex(-x3-x2-x+1)+ex(-3x2-2x-1)=-x(x+1)(x+3)ex,
令g′(x)=0,得x1=-3,x2=-1,x3=0,
可得g(x)在区间(-∞,-3),(-1,0)单调递增,在区间(-3,-1)(0,+∞)单调递减,
所以g(x)在x=-3时取极大值g(-3)=
| 22 |
| e3 |
| 2 |
| e |
又
| 22 |
| e3 |
| 22 |
| e3 |
如图,过点P(0,t)有且只有一条直线与曲线f(x)相切等价于直线y=t与曲线g(x)=ex(-x3-x2-x+1)有且只有一个交点,又当x<-3时,g(x)>0,
所以t=
| 22 |
| e3 |
故答案为:t=
| 22 |
| e3 |
点评:考查学生利用导数研究函数的单调性的能力,以及利用导数研究曲线上某点切线方程的能力.会用数形结合的数学思想解决数学问题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
复数
的共轭复数是( )
| i+1 |
| 1-i |
| A、2 | B、i | C、-i | D、-2i |
 如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ACB=β.
如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ACB=β.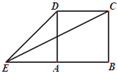 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=