题目内容
9.已知f(x)=4sinαcosα-5sinα-5cosα.(1)若f(x)=1,求sinα+cosα的值;
(2)当$α∈[{0,\frac{π}{2}}]$时,求f(x)的值域.
分析 (1)令sinα+cosα=t,换元平方得2sinα•cosα=t2-1,由此利用二次函数和三角函数的性质能求出sinα+cosα的值.
(2)令t=sinα+cosα,推导出$t∈[{1,\sqrt{2}}]$,由此利用二次函数性质能求出f(x)的值域.
解答 解:(1)令sinα+cosα=t,换元平方得2sinα•cosα=t2-1,
∵f(x)=1,∴2(t2-1)-5t=1,
即2t2-5t-3=0,解得$t=-\frac{1}{2}或t=3$
又∵$t=sinα+cosα=\sqrt{2}sin({α+\frac{π}{4}})∈[{-\sqrt{2},\sqrt{2}}]$,
∴$t=-\frac{1}{2},即sinα+cosα=-\frac{1}{2}$
(2)令t=sinα+cosα,
∵$sinα+cosα=\sqrt{2}sin({α+\frac{π}{4}}),α∈[{0,\frac{π}{2}}]$,
∴$α+\frac{π}{4}∈[{\frac{π}{4},\frac{3π}{4}}],sin({α+\frac{π}{4}})∈[{\frac{{\sqrt{2}}}{2},1}]$,
即$t∈[{1,\sqrt{2}}]$,
∴$f(x)=2{t^2}-5t-2,t∈[{1,\sqrt{2}}]$,
由二次函数图象可知:$f(x)∈[{-\frac{41}{8},-5}]$.
点评 本题考查函数值和函数的值域的求法,是中档题,解题时要认真审题,注意换元法的合理运用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
19.执行如图所示的程序框图,输出P的值为( )


| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
17.已知点F1,F2分别是双曲线x2-$\frac{{y}^{2}}{24}$=1的左右焦点,P为该双曲线上一点,且|PF1|=$\frac{4}{3}$|PF2|,则△F1PF2的面积为( )
| A. | $\frac{24}{49}$ | B. | 12 | C. | $\frac{12}{49}$ | D. | 24 |
14.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
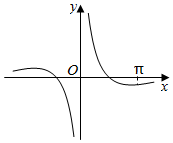

| A. | $f(x)=\frac{{2-{x^2}}}{2x}$ | B. | $f(x)=\frac{sinx}{x^2}$ | C. | $f(x)=-\frac{{{{cos}^2}x}}{x}$ | D. | $f(x)=\frac{cosx}{x}$ |