题目内容
4.设a∈R,函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+a,x≥0}\\{g(x),x<0}\end{array}\right.$为奇函数,则a=-1,f(x)+3=0的解为-2.分析 根据函数奇偶性的性质建立方程关系进行求解即可.
解答 解:∵函数f(x)是奇函数,
∴f(0)=0,则20+a=1+a=0,得a=-1,
若x<0,则-x>0,
则f(-x)=2-x-1=-f(x),
则f(x)=1-2-x,x<0,
即g(x)=1-2-x,x<0,
由f(x)+3=0得f(x)=-3,
若x≥0,由f(x)=-3得2x-1=-3,得2x=-2,此时方程无解,
若x<0,由f(-x)=-3得1-2-x=-3,
得2-x=4,即-x=2,得x=-2,
故答案为:-2
点评 本题主要考查函数奇偶性的应用,根据函数奇偶性的性质建立方程关系是解决本题的关键.

练习册系列答案
相关题目
15.将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向左平移φ(φ>0)个单位后,得到的函数图象关于y轴对称,则φ的最小值为( )
| A. | $\frac{5}{8}$π | B. | $\frac{3}{8}$π | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
19.设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数f′(x),且f′(x)是偶函数,则曲线y=f(x)在点(2,f(2))处的切线方程为( )
| A. | 9x+y+16=0 | B. | 9x-y-16=0 | C. | 9x-y+16=0 | D. | 9x+y-16=0 |
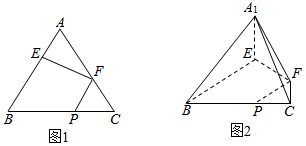 在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点满足AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF折起到△A1EF的位置上,连接A1B,A1C(如图2)
在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点满足AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF折起到△A1EF的位置上,连接A1B,A1C(如图2)