题目内容
1．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$+$\overrightarrow{b}$=（1，-3），$\overrightarrow{a}$-$\overrightarrow{b}$=（3，7），$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）| A． | -12 | B． | -20 | C． | 12 | D． | 20 |
分析 求出两向量的坐标，代入数量积的坐标运算即可．
解答 解：∵$（\overrightarrow{a}+\overrightarrow{b}）+（\overrightarrow{a}-\overrightarrow{b}）=2\overrightarrow{a}$=（4，4），
∴$\overrightarrow{a}=（2，2）$，∴$\overrightarrow{b}=（\overrightarrow{a}+\overrightarrow{b}）-\overrightarrow{a}$=（-1，-5）．
∴$\overrightarrow{a}•\overrightarrow{b}$=2×（-1）-2×5=-12．
故选A．
点评 本题考查了平面向量的数量积运算，属于基础题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
11．△ABC中，AB=5，BC=3，CA=7，若点D满足$\overrightarrow{BD}=2\overrightarrow{DC}$，则△ABD的面积为（ ）
| A． | $\frac{{5\sqrt{3}}}{2}$ | B． | $\frac{5}{2}$ | C． | $5\sqrt{3}$ | D． | 5 |
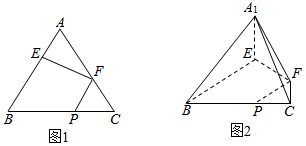在正三角形ABC中，E，F，P分别是AB，AC，BC边上的点满足AE：EB=CF：FA=CP：PB=1：2（如图1），将△AEF折起到△A1EF的位置上，连接A1B，A1C（如图2）