题目内容
设a+2b=3,b>0,则
+
的最小值为 .
| 1 |
| 2|a| |
| |a| |
| 3b |
考点:基本不等式
专题:导数的综合应用,不等式的解法及应用
分析:由a+2b=3,b>0,可得a=3-2b≠0.于是得到
+
=
+
=f(b).通过对a分类讨论,利用导数研究函数的单调性极值与最值即可.
| 1 |
| 2|a| |
| |a| |
| 3b |
| 1 |
| 2|3-2b| |
| |3-2b| |
| 3b |
解答:
解:∵a+2b=3,b>0,
∴a=3-2b≠0
∴
+
=
+
=f(b).
当b>
时,f(b)=
+
,则f′(b)=
+
=
,
当
<b<3时,f′(b)<0,函数f(b)单调递减;当b>3时,f′(b)>0,函数f(b)的单调递增.
又f′(3)=0,∴当b=3时,函数f(b)取得极小值,f(3)=
.
当0<b<
时,f(b)=
+
,
则f′(b)=-
,此时当b=1时,f(b)取得极小值,f(1)=
.
综上可知:当b=3时,函数f(b)取得最小值,f(3)=
.
故答案为:
.
∴a=3-2b≠0
∴
| 1 |
| 2|a| |
| |a| |
| 3b |
| 1 |
| 2|3-2b| |
| |3-2b| |
| 3b |
当b>
| 3 |
| 2 |
| 1 |
| 2(2b-3) |
| 2b-3 |
| 3b |
| -1 |
| (2b-3)2 |
| 1 |
| b2 |
| 3(b-1)(b-3) |
| (2b2-3b)2 |
当
| 3 |
| 2 |
又f′(3)=0,∴当b=3时,函数f(b)取得极小值,f(3)=
| 1 |
| 2 |
当0<b<
| 3 |
| 2 |
| 1 |
| 2(3-2b) |
| 3-2b |
| 3b |
则f′(b)=-
| 3(b-1)(b-3) |
| (2b2-3b)2 |
| 5 |
| 6 |
综上可知:当b=3时,函数f(b)取得最小值,f(3)=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值、分类讨论,属于中档题.

练习册系列答案
相关题目
已知i为虚数单位,若复数z满足z(i-2)=1+2i,则z的共轭复数是( )
| A、i | ||
| B、-i | ||
C、
| ||
D、-
|
 如图是某公司10个销售店某月销售某品牌电脑数量(单位:台)的茎叶图,则数
如图是某公司10个销售店某月销售某品牌电脑数量(单位:台)的茎叶图,则数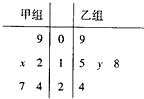 如图方茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为l5,乙组数据的平均数为16.8,则x+y的值为
如图方茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为l5,乙组数据的平均数为16.8,则x+y的值为