题目内容
19.已知集合A={x|x2-x-2≤0},集合B={x|m≤x<m+5,m∈R}.(Ⅰ)若m=0,求A∩B.
(Ⅱ)若A∩B=∅,求实数m的取值范围.
分析 (Ⅰ)求出m=0时的集合B,由二次不等式的解法可得集合A,再由交集的定义可得所求集合;
(Ⅱ)若A∩B=∅,则m+5≤-1或m>2,解不等式即可得到所求m的范围.
解答 解:(Ⅰ)若m=0,则集合B={x|0≤x<5},
集合A={x|x2-x-2≤0}={x|-1≤x≤2},
则A∩B={x|0≤x≤2};
(Ⅱ)若A∩B=∅,则m+5≤-1或m>2,
即m≤-6或m>2,
则实数m的取值范围是(-∞,-6]∪(2,+∞).
点评 本题考查集合的交集的运算,考查二次不等式的解法,注意运用定义法是解题的关键,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.若a,b,c为实数,且a>b,则下列不等式一定成立的是( )
| A. | ac>bc | B. | a-b>b-c | C. | a+c>b+c | D. | a+c>b |
10. 如图一铜钱的直径为32毫米,穿径(即铜钱内的正方形小孔边长)为8毫米,现向该铜钱内随机地投入一粒米(米的大小忽略不计),则该粒米未落在铜钱的正方形小孔内的概率为( )
如图一铜钱的直径为32毫米,穿径(即铜钱内的正方形小孔边长)为8毫米,现向该铜钱内随机地投入一粒米(米的大小忽略不计),则该粒米未落在铜钱的正方形小孔内的概率为( )
 如图一铜钱的直径为32毫米,穿径(即铜钱内的正方形小孔边长)为8毫米,现向该铜钱内随机地投入一粒米(米的大小忽略不计),则该粒米未落在铜钱的正方形小孔内的概率为( )
如图一铜钱的直径为32毫米,穿径(即铜钱内的正方形小孔边长)为8毫米,现向该铜钱内随机地投入一粒米(米的大小忽略不计),则该粒米未落在铜钱的正方形小孔内的概率为( )| A. | $\frac{1}{4π}$ | B. | $1-\frac{1}{4π}$ | C. | $\frac{1}{2π}$ | D. | $1-\frac{1}{6π}$ |
14.已知集合A={1,2,3,4,5},B={3,4,5,6,7},则图中阴影部分表示的集合为( )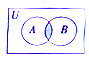

| A. | {1,2,3,4,5} | B. | {3,4,5,6,7} | C. | {1,2,3,4,5,6,7} | D. | {3,4,5} |
11.已知直线l1:(m-4)x-(2m+4)y+2m-4=0与l2:(m-1)x+(m+2)y+1=0,则“m=-2”是“l1∥l2”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分又不必要 |
8.函数y=$\frac{lg|x|}{x}$的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
9.设集合A={x|-1<x<3},B={x|x≥1},则A∩B=( )
| A. | (-1,1] | B. | [1,3) | C. | [-1,3] | D. | (-1,+∞) |