题目内容
(本小题满分14分)设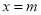 和
和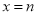 是函数
是函数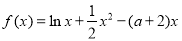 的两个极值点,其中
的两个极值点,其中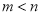 ,
,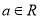 .
.
(1)若曲线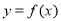 在点
在点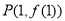 处的切线垂直于
处的切线垂直于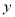 轴,求实数
轴,求实数 的值;
的值;
(2)求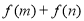 的取值范围;
的取值范围;
(3)若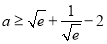 ,求
,求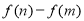 的最大值(
的最大值(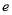 是自然对数的底数).
是自然对数的底数).
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)结合导数的几何意义,可知 在
在 处的切线垂直于
处的切线垂直于 轴等价于
轴等价于 ,从而可列出关于
,从而可列出关于 的方程,即可求得
的方程,即可求得 的值;
的值;
(2)由条件 和
和 是函数
是函数 的两个极值点且
的两个极值点且 可知方程
可知方程 有两个不等的正根
有两个不等的正根 ,
, ,则
,则 ,
, ,再由一元二次方程根的分布可得
,再由一元二次方程根的分布可得 ,从而
,从而
 ,故
,故 的取值范围是
的取值范围是 ;
;
(3)由(2)可知
 ,
,
因此可令 ,根据条件
,根据条件 可得
可得 ,从而
,从而 ,
,
构造函数 (其中
(其中 ),问题即等价于在函数
),问题即等价于在函数 在
在 上的最大值,利用导数判断其单调性即可求得
上的最大值,利用导数判断其单调性即可求得 的最大值. .
的最大值. .
试题解析:(1)∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ;(2)函数
;(2)函数 的定义域为
的定义域为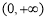 ,
, ,
,
依题意,方程 有两个不等的正根
有两个不等的正根 ,
, (其中
(其中 ),故
),故 ,
,
且 ,
, ,∴
,∴
 ,故
,故 的取值范围是
的取值范围是 ;
;
(3)当 时,
时, ,若设
,若设 ,则
,则
 ,于是有
,于是有 ,
,

 ,
,
构造函数 (其中
(其中 ),则
),则 ,
,
∴ 在
在 上单调递减,
上单调递减, ,故
,故 的最大值是
的最大值是 .
.
考点:1.利用导数研究函数的极值;2.利用导数求函数在给定区间上的值域;3.一元二次方程根的分布.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 ,记
,记 ,若函数
,若函数 至少存在一个零点,则实m数拼的取值范围是( )
至少存在一个零点,则实m数拼的取值范围是( ) B.
B.
 D.
D.

 (B)
(B) (C)
(C) (D)
(D)
 的图像在点
的图像在点 处的切线方程为 .
处的切线方程为 . 
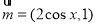 ,
,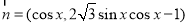 ,函数
,函数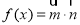 .
.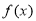 的单调递增区间;
的单调递增区间;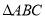 中,角
中,角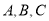 的对边分别为
的对边分别为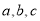 ,若
,若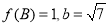 ,
, ,求
,求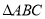
 的焦点为
的焦点为 ,准线为
,准线为 ,点
,点 为抛物线上任意一点,且在第一象限,
为抛物线上任意一点,且在第一象限,
 ,垂足为
,垂足为 ,
, ,则直线
,则直线 的倾斜角等于( )
的倾斜角等于( ) B.
B. C.
C. D.
D.
 在不等式组
在不等式组 表示的平面区域内,若点
表示的平面区域内,若点 到直线
到直线 的最大距离为
的最大距离为 ,则实数
,则实数 .
.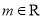 ,则“
,则“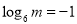 ”是“直线
”是“直线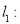
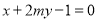 与
与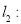
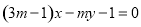 平行”的( )
平行”的( )